题目内容
9.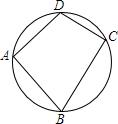 如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.
如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.
分析 连接BD,根据圆内接四边形对角互补可得∠A=90°,根据90°的圆周角所对的弦是直径可得BD是直径,再利用勾股定理计算出BD长即可.
解答  解:连接BD,
解:连接BD,
∵点A、B、C、D在同一个圆上,
∴∠A+∠C=180°,
∵∠A=90°,
∴∠C=90°,
∴BD就是直径,
∵CD=2,BC=3,
∴BD=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
故答案为:$\sqrt{13}$.
点评 此题主要考查了圆周角定理,圆内接四边形的性质,以及勾股定理,关键是掌握圆内接四边形对角互补,90°的圆周角所对的弦是直径.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
18.扬州商场某商家计划购进一批甲、乙两种LED节能灯共120只,这两种节能灯的进价、售价如下表:
(1)如果进货总费用恰好为4600元,请你设计出进货方案.
(2)如果规定:当销售完这批节能灯后,总利润不超过进货总费用的30%,请问如何进货,使得该商家获得的总利润最多,此时总利润最多为多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)如果规定:当销售完这批节能灯后,总利润不超过进货总费用的30%,请问如何进货,使得该商家获得的总利润最多,此时总利润最多为多少元?
 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 如图,在矩形ABCD中,AB=2cm,BC=4cm,动点M从点A出发,以1cm/s的速度沿AB向点B运动;在点M出发的同时,动点N从点B出发,以2cm/s的速度沿BC向点C运动,当点M到达点B时,运动停止.设运动时间为t(s),则当t为何值时,△BMN的面积S(cm2)最大?最大值为多少?
如图,在矩形ABCD中,AB=2cm,BC=4cm,动点M从点A出发,以1cm/s的速度沿AB向点B运动;在点M出发的同时,动点N从点B出发,以2cm/s的速度沿BC向点C运动,当点M到达点B时,运动停止.设运动时间为t(s),则当t为何值时,△BMN的面积S(cm2)最大?最大值为多少?