题目内容
17.(1)计算:3$\sqrt{24}$-$\sqrt{\frac{1}{6}}$-$\sqrt{600}$(2)解方程组:$\left\{\begin{array}{l}{3x-2y=-19}\\{x-5y=-2}\end{array}\right.$.
分析 (1)先把各根式化为最减二次根式,再合并同类项即可;
(2)先用加减消元法求出y的值,再用代入消元法求出x的值即可.
解答 解:(1)原式=6$\sqrt{6}$-$\frac{\sqrt{6}}{6}$-10$\sqrt{6}$
=(6-$\frac{1}{6}$-10)$\sqrt{6}$
=-$\frac{25\sqrt{6}}{6}$;
(2)$\left\{\begin{array}{l}3x-2y=-19①\\ x-5y=-2②\end{array}\right.$,①-②×3得,13y=-13,解得y=-1,把y=-1代入②得,x+5=-2,解得x=-7,
故方程组的解为$\left\{\begin{array}{l}x=-7\\ y=-1\end{array}\right.$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
12.在平面直标坐标系中,点P(-3,-5)关于y轴对称点的坐标为( )
| A. | (-3,-5) | B. | (3,5) | C. | (3,-5) | D. | (5,-3) |
6.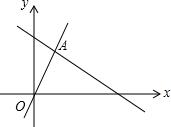 如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
 如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )| A. | x<1 | B. | x>1 | C. | x≥1 | D. | x≤1 |
7.把分式$\frac{b}{a}$中的a,b都扩大3倍,则分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 扩大6倍 | D. | 缩小3倍 |
 如图,在平面直角坐标系中xOy,二次函数y=ax2-2ax+3的图象与x轴分别交于点A、B,与y轴交于点C,AB=4,动点P从B点出发,沿x轴负方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线BC,垂足为Q.设P点移动的时间为t秒(t>0),△BPQ与△ABC重叠部分的面积为S.
如图,在平面直角坐标系中xOy,二次函数y=ax2-2ax+3的图象与x轴分别交于点A、B,与y轴交于点C,AB=4,动点P从B点出发,沿x轴负方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线BC,垂足为Q.设P点移动的时间为t秒(t>0),△BPQ与△ABC重叠部分的面积为S. 如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问
如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问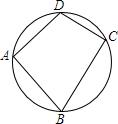 如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.
如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.