题目内容
1.已知关于x的不等式$\frac{x}{a}$<7的解都能使关于x的不等式$\frac{2x-7}{5}$>$\frac{a}{2-1}$成立,a的取值范围是什么?分析 先把a看作常数求出两个不等式的解集,再根据同小取小列出不等式求解即可.
解答 解:解不等式$\frac{x}{a}$<7得:当a>0时,x<7a;当a<0时,x>7a
解不等式$\frac{2x-7}{5}$>$\frac{a}{2-1}$得:$x>\frac{5a+7}{2}$,
因为关于x的不等式$\frac{x}{a}$<7的解都能使关于x的不等式$\frac{2x-7}{5}$>$\frac{a}{2-1}$成立,
所以可得:7a≤$\frac{5a+7}{2}$,且a<0,
所以a的取值范围是a<0.
点评 本题考查了解一元一次不等式,分别求出两个不等式的解集,再根据同小取小列出关于a的不等式是解题的关键.

练习册系列答案
相关题目
12.下列式子中是完全平方式的是( )
| A. | a2+2ab+b2 | B. | a2+2a+2 | C. | a2-2b+b2 | D. | a2+2a+b2 |
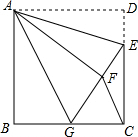 如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②AG∥CF;③sin∠EGC=$\frac{4}{5}$;④S△AGE=15.其中正确的结论是①②③④.(只填序号)
如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②AG∥CF;③sin∠EGC=$\frac{4}{5}$;④S△AGE=15.其中正确的结论是①②③④.(只填序号)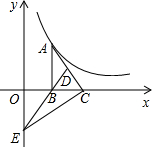 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.