题目内容
10.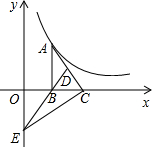 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
分析 连结OA、EA,如图,根据三角形面积公式,由AD=2CD得到S△ADE=2S△CDE,S△ADB=2S△CDB,则S△ABE=2S△BCE=4,再根据三角形面积公式得到S△ABE=SOAB=4,然后根据反比例函数的比例系数k的几何意义得到$\frac{1}{2}$×|k|=4,然后去绝对值即可得到满足条件的k的值.
解答 解: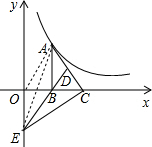 连结OA、EA,如图,
连结OA、EA,如图,
∵AD=2CD,
∴S△ADE=2S△CDE,S△ADB=2S△CDB,
即S△ABE+S△ADE=2(S△CDB+S△BCE),
∴S△ABE=2S△BCE=2×2=4,
∵OE∥AB,
∴S△ABE=SOAB=4,
∴$\frac{1}{2}$×|k|=4,
而k>0,
∴k=8.
故答案为8.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了三角形面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列运算正确的是( )
| A. | x3•x2=x5 | B. | (x3)3=x6 | C. | x5+x5=x10 | D. | x4-x2=x2 |
15.下面是某校八年级(2)班两组女生的体重(单位:kg).
(1)分别求这两组数据的平均数、众数、中位数,并解释它们的实际意义(结果保留整数);
(2)比较两组数据的平均数、众数、中位数,并谈谈对它们的认识.
| 第1组 | 35 | 36 | 38 | 40 | 42 | 42 | 75 |
| 第2组 | 35 | 36 | 38 | 40 | 42 | 42 | 45 |
(2)比较两组数据的平均数、众数、中位数,并谈谈对它们的认识.
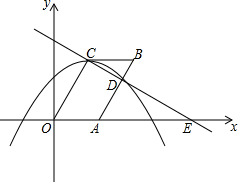 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.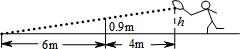 在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.
在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.