题目内容
16.在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E.如果DE过重心G点,且DE=4,那么BC的长是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 如图,连结AG并延长交BC于F,根据三角形重心性质得$\frac{AG}{GF}$=2,再证明△ADE∽△ABC,根据相似三角形的性质得$\frac{DE}{BC}$=$\frac{AG}{AF}$,然后利用比例的性质计算BC的长.
解答 解:如图, 连结AG并延长交BC于F,如图,
连结AG并延长交BC于F,如图,
∵点G为△ABC的重心,
∴$\frac{AG}{GF}$=2,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AG}{AF}$,即$\frac{4}{BC}$=$\frac{2}{2+1}$,
∴BC=6.
故选B.
点评 本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
6.下列条件中,可以确定△ABC和△A′B′C′全等的是( )
| A. | BC=BA,B′C′=B′A′,∠B=∠B′ | B. | ∠A=∠B′,AC=A′B′,AB=B′C′ | ||
| C. | ∠A=∠A′,AB=B′C′,AC=A′C′ | D. | BC=B′C′,AC=A′B′,∠B=∠C′ |
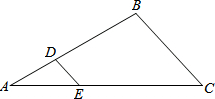 如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.
如图,在△ABC中,DE∥BC,AD=3,BD=6,AE=4,则EC的长是8.
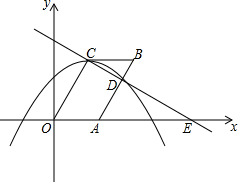 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.