题目内容
18.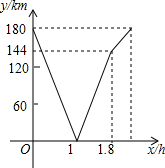 一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.
一辆货车从A地去B地,一辆轿车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,轿车的速度大于货车的速度.两辆车之间的距离为y(km)与货车行驶的时间为x(h)之间的函数关系如图所示.(1)求轿车的速度.
(2)求轿车到达A地后y与x之间的函数关系式.
(3)当两车相遇后,求两车相距160km时货车行驶的时间.
分析 (1)由图象可知,A、B两地相距180km,轿车行驶全程用时1.8h,可得答案;
(2)根据轿车、货车行驶1h相遇求得货车速度,继而可得货车到达B地时间,待定系数法可得函数解析式;
(3)由图象知,当1≤x≤1.8时,两车间的距离最大为144km,可得当1.8<x≤2.25时距离可以达到160km,由(2)函数解析式可得方程,解方程可得x的值.
解答 解:(1)轿车的速度是180÷1.8=100km/h.
(2)货车的速度是$\frac{180-100×1}{1}$=80km/h.
∴$\frac{180}{80}$=2.25.
设y与x之间的函数关系式为y=kx+b.
由题意,得$\left\{\begin{array}{l}{1.8k+b=144}\\{2.25k+b=180}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=80}\\{b=0}\end{array}\right.$,
∴轿车到达A地后y与x之间的函数关系式为y=80x.
(3)当y=160时,80x=160.
解得:x=2.
答:两车相距160km时货车行驶了2h.
点评 本题主要考查一次函数的图象、待定系数法求函数解析式及其应用,理解题意求得货车速度及货车到达终点的时间是求函数解析式的关键.

练习册系列答案
相关题目
11.分解因式:16-x2=( )
| A. | (4-x)(4+x) | B. | (x-4)(x+4) | C. | (8+x)(8-x) | D. | (4-x)2 |
13.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)如果物体的质量为x kg,弹簧长度为y cm,根据上表写出y与x的关系式;
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
| 所挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(2)当物体的质量为2.5kg时,根据(1)的关系式,求弹簧的长度;
(3)当弹簧的长度为17cm时,根据(1)的关系式,求弹簧所挂物体的质量.
10.一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行90km所用时间,与以最大航速逆流航行60km所用时间相等.设江水的流速为vkm/h,根据题意,下列所列方程正确的是( )
| A. | $\frac{90}{30+v}=\frac{60}{30-v}$ | B. | $\frac{90}{v}=\frac{60}{30-v}$ | C. | $\frac{90}{30-v}=\frac{60}{30+v}$ | D. | $\frac{90}{30-v}=\frac{60}{v}$ |
7.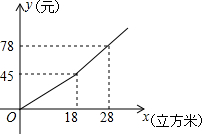 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
(1)根据图象,求出y关于x的函数表达式.
(2)请根据自来水公司在这两个用水范围内的收费标准,计算以下各家应交的水费,直接填入下表:
(3)若某用户计划某个月水费不超过51.6元,则这个月最多可用多少立方米水?
 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.(1)根据图象,求出y关于x的函数表达式.
(2)请根据自来水公司在这两个用水范围内的收费标准,计算以下各家应交的水费,直接填入下表:
| 用水量/立方米 | 水费/元 | |
| 小刚 | 15 | 37.5 |
| 小丽 | 25 | 68.1 |

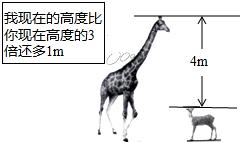 如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.
如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.