题目内容
11．解方程：（1）$\frac{x}{x-2}$-$\frac{4}{{x}^{2}-4}$=1．
（2）$\frac{x}{x-1}$-1=$\frac{3}{（x-1）（x+2）}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可确定出分式方程的解．
解答 解：（1）去分母得：x2+2x-4=x2-4，
解得：x=0，
经检验x=0是分式方程的解；
（2）去分母得：x2+2x-x2-x+2=3，
解得：x=1，
经检验x=1是增根，分式方程无解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
提分百分百检测卷系列答案
相关题目
19．
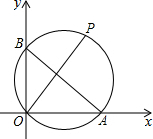如图，点A的坐标为A（8，0），点B在y轴正半轴上，且AB=10，点P是△AOB外接圆上一点，且∠BOP=45°，则点P的坐标为（ ）
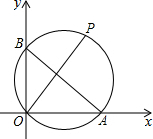如图，点A的坐标为A（8，0），点B在y轴正半轴上，且AB=10，点P是△AOB外接圆上一点，且∠BOP=45°，则点P的坐标为（ ）| A． | （7，7） | B． | （7$\sqrt{2}$，7$\sqrt{2}$） | C． | （5$\sqrt{2}$，5$\sqrt{2}$） | D． | （5，5） |
如图，已知在正方形ABCD中，点E，G分别在边BC，CD上，且AE=AF．求证：CE=CF．
如图所示，AB∥CD，O为∠A、∠C的平分线的交点，OE⊥AC于E，且OE=4，则AB与CD之间的距离等于8．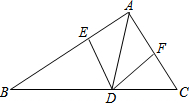
如图，已知S△ABC=40，AB=22，AC=18，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，则DE=2．