题目内容
设x1,x2是一元二次方程x2+5x-3=0的两根,且2x1(x22+6x2-3)+a=4,则a= .
考点:根与系数的关系
专题:计算题
分析:先根据一元二次方程根的定义得到x22+5x2-3=0,则x22+5x2=3,由于2x1(x22+6x2-3)+a=4,则2x1•x2+a=4,然后根据根与系数的关系得x1x2=-3,
所以2×(-3)+a=4,再解一次方程即可.
所以2×(-3)+a=4,再解一次方程即可.
解答:解:∵x2是一元二次方程x2+5x-3=0的根,
∴x22+5x2-3=0,
∴x22+5x2=3,
∵2x1(x22+6x2-3)+a=4,
∴2x1•x2+a=4,
∵x1,x2是一元二次方程x2+5x-3=0的两根,
∴x1x2=-3,
∴2×(-3)+a=4,
∴a=10.
∴x22+5x2-3=0,
∴x22+5x2=3,
∵2x1(x22+6x2-3)+a=4,
∴2x1•x2+a=4,
∵x1,x2是一元二次方程x2+5x-3=0的两根,
∴x1x2=-3,
∴2×(-3)+a=4,
∴a=10.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,用直尺和圆规画出∠ABC的平分线BM,
如图,用直尺和圆规画出∠ABC的平分线BM,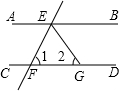 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=