题目内容
20. 如图:在△ABC中,BD、CE分别是△ABC边AC、AB上的高,直线BD、CE相交于H.
如图:在△ABC中,BD、CE分别是△ABC边AC、AB上的高,直线BD、CE相交于H.(1)若∠A=60°,求∠BHC的度数?
(2)猜想,∠BHC与∠A互补吗?并说明理由?
(3)若∠A为钝角时,上述关系还存在吗?试通过画图说明是否存在这种关系.(不必说明理由)
分析 (1)根据高的定义得∠ADB=∠AEC=90°,于是利用四边形内角和为360°可计算出∠EHD,然后根据对顶角相等得到∠BHC的度数;
(2)利用(1)中的四边形的内角和和高的意义判定即可;
(3)利用(2)中的结论和过程说明∠BHC与∠A互补.
解答 解:(1)∵BD、CE分别是△ABC边AC、AB上的高,
∴∠ADB=∠AEC=90°,
而∠A+∠AEH+∠ADH+∠EHD=360°,
∴∠EHD=180°-60°=120°,
∴∠BHC=120°.
(2)∠A与∠BHC互补.
理由:∵∠A+∠AEH+∠ADH+∠EHD=360°,∠ADB=∠AEC=90°,
∴∠A+∠BHC=180°.
(3)∠BAC+∠EHD=180°.
∵BD,CE是△ABC的高(已知),
∴∠ADH=∠AEH=90°(高的意义),
∵∠DAE+∠AEH+∠ADH+∠EHD=360°,∠DAE=∠BAC,
∴∠BAC+∠EHD=180°.
如图,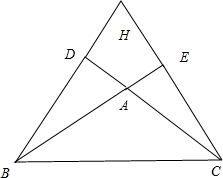
点评 本题考查了三角形内角和定理,四边形的内角和以及三角形高的意义,解答此类题目要注意三角形的内角和是180°这一隐含的条件来解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.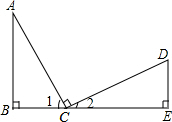 已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠1=∠2 |
10.反比例函数y=$\frac{m-3}{x}$的图象,当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
 如图,B、C是线段AD上的任意两点,M是AB的中点,N是CD的中点,如果MN=3cm,BC=1.5cm,求AD的长.
如图,B、C是线段AD上的任意两点,M是AB的中点,N是CD的中点,如果MN=3cm,BC=1.5cm,求AD的长.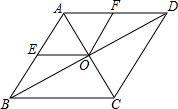 平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形.
平行四边形ABCD的对角线AC,BD相交于点O,AE=EB,OF=$\frac{1}{2}$CD,求证:四边形AEOF为平行四边形.