题目内容
15.如图,已知△ABC中,∠ACB=90°,∠ABC=30°,AC=2,点P是边AB上的一个动点,以点P为圆心,PB的长为半径画弧,交射线BC于点D,射线PD交射线AC于点E.(1)当点D与点C重合时,求PB的长;
(2)当点E在AC的延长线上时,设PB=x,CE=y,求y关于x的函数关系式,并写出定义域;
(3)当△PAD是直角三角形时,求PB的长.
分析 (1)根据直角三角形的性质得到AC=$\frac{1}{2}$AB,根据等腰三角形的性质得到∠PCB=∠B=30°,根据等边三角形的性质即可得到结论;
(2)由等腰三角形的性质得到∠PDB=∠B=30°,求得AE=AP,即可得到结论;
(3)①如图2,当点E在AC的延长线上时,求得∠PDA=90°,根据直角三角形的性质得到PD=$\frac{1}{2}$AP,解方程得到x=$\frac{4}{3}$;②如图3,当点E在AC边上时,根据直角三角形的性质得到AP=$\frac{1}{2}$PD.解方程得到x=$\frac{8}{3}$.
解答 解: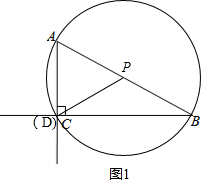 (1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,
(1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,
∴AC=$\frac{1}{2}$AB,
∵AC=2,
∴AB=4,
∵以点P为圆心,PB的长为半径画弧,交射线BC于点D,点D与点C重合,
∴PD=PB,
∴∠PCB=∠B=30°,
∴∠APC=∠ACD=60°,
∴AP=AC=2,
∴BP=2;
(2)∵PD=PB,∠ABC=30°,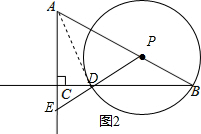
∴∠PDB=∠B=30°,
∴∠APE=60°,∠CDE=30°,
∵∠ACD=90°,
∴∠AEP=60°,
∴AE=AP,
∵PB=x,CE=y,
∴2+y=4-x,y=2-x.(0<x<2);
(3)①如图2,当点E在AC的延长线上时,连接AD,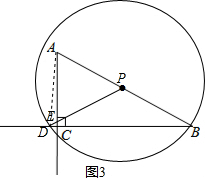
∵△PAD是直角三角形,∠APD=60°,∠PAD<60°,
∴∠PDA=90°,
∴∠PAD=30°.
∴PD=$\frac{1}{2}$AP,
即x=$\frac{1}{2}$(4-x),
∴x=$\frac{4}{3}$;
②如图3,当点E在AC边上时,连接AD
∵△PAD是直角三角形,∠APD=60°,∠ADP<60°,
∴∠PAD=90°,
∴∠PDA=30°.
∴AP=$\frac{1}{2}$PD.即4-x=$\frac{1}{2}$x,
∴x=$\frac{8}{3}$.
综上所述:当PB的长是$\frac{4}{3}$或$\frac{8}{3}$时,△PAD是直角三角形.
点评 本题考查了直角三角形的判定和性质,圆的性质,求函数的解析式,等边三角形的性质,熟练掌握各性质定理是解题的关键.

| 姓名 | A | B | C | D | E | F | G | H | I |
| 成绩(米) | 0.91 | 0.95 | 1.10 | 0.98 | 1.08 | 0.96 | 1.12 | 1.18 | 1.17 |
(2)分别求出这组数据的平均数和中位数.
(3)你认为哪个数据代表这组数据的一般水平更合适?
(4)如果再增加一个同学的成绩是1.15米,这组数据的中位数是多少?
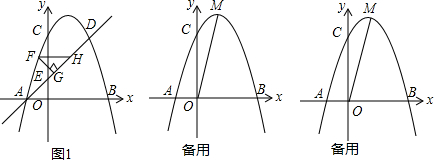
 如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
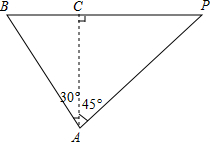 如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).
如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).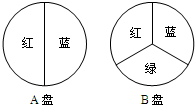 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?请你并说明理由.