题目内容
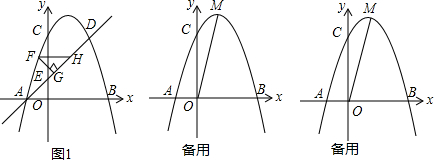
6.如图,抛物线y=-x2+2x+3与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C.点D和点C关于抛物线的对称轴对称,直线AD与y轴相交于点E.(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH的周长的最大值;
(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.
分析 (1)求出A、D两点坐标,利用待定系数法即可解决问题.
(2)首先证明△FHG是等腰直角三角形,构建二次函数利用函数性质解决问题即可.
(3)分两种情形①如图2中,若AP为对角线,利用相似三角形性质求出点T坐标.②如图3中,若AQ为对角线,利用相似三角形性质即可解决问题.
解答 解:(1)∵抛物线y=-x2+2x+3与x轴交与A,B两点(点A在点B的左侧),与y轴交于点C,
∴点A坐标(-1,0),点B坐标(3,0),点C坐标(0,3),
∵抛物线对称轴x=1,D、C关于对称轴对称,
∴点D坐标(2,3),设直线AD为y=kx+b.则$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=3}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$;
∴直线AD解析式为:y=x+1.
(2)如图1中,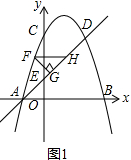
∵OA=OE=1,
∴∠EAO=45°,
∵FH∥AB,
∴∠FHA=∠EAO=45°,
∵FG⊥AH,
∴△FGH是等腰直角三角形,
设点F坐标(m,-m2+2m+3),
∴点H坐标(-m2+2m+2,-m2+2m+3),
∴FH=-m2+m+2,
∴△FGH的周长=(-m2+m+2)+2×$\frac{\sqrt{2}}{2}$(-m2+m+2)=-(1+$\sqrt{2}$)(m-$\frac{1}{2}$)2+$\frac{9+9\sqrt{2}}{4}$
∴△FGH的周长最大值为$\frac{9+9\sqrt{2}}{4}$.
(3)①如图2中,若AP为对角线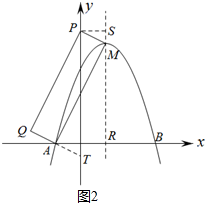
作PS⊥对称轴于于S,对称轴与x轴的交点为R,
∵∠PMS+∠MPS=90°,∠PMS+∠AMR=90°,
∴∠MPS=∠AMR,∵∠PSM=∠MRA,
∴△PMS∽△MAR可得$\frac{PS}{MR}$=$\frac{SM}{AR}$,
∴$\frac{1}{4}$=$\frac{SM}{2}$,
∴SM=$\frac{1}{2}$,
∴点P坐标(0,$\frac{9}{2}$)
由点的平移可知Q(-2,$\frac{1}{2}$)
故Q点关于直线AM的对称点T为(0,-$\frac{1}{2}$).
②如图3中,若AQ为对角线,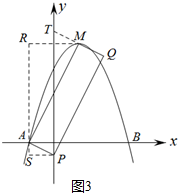
作AR∥y轴,MR∥x轴,AS∥y轴,PS∥AB,
同理可证△ARM∽△PSA,
∴$\frac{AR}{PS}$=$\frac{RM}{AS}$,
∴AS=$\frac{1}{2}$
∴点P坐标(0,-$\frac{1}{2}$),
由点的平移可知Q(2,$\frac{7}{2}$),
故Q点关于直线AM的对称点T为(0,$\frac{9}{2}$).
点评 本题考查二次函数的性质、一次函数、矩形的性质、平移、对称等知识,解题的关键是添加常用辅助线构造相似三角形,属于中考压轴题.

 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):88,85,90,99,86,68,94,98,78,97
96,93,89,94,89,85,80,95,89,77
请根据上述数据,解决下列问题:
(1)补全下面考生素描成绩的表格(每组数据含最小值不含最大值)和频数分布直方图;
| 分组 | 人数(频数) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
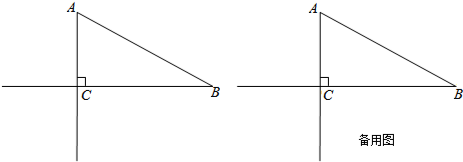
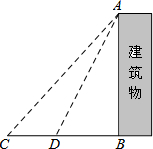 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
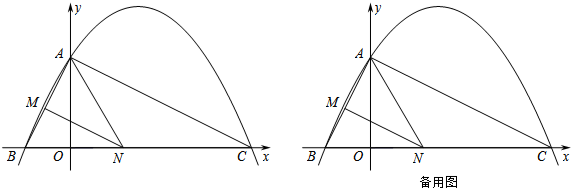
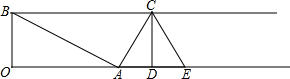 如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.
如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.