题目内容
17.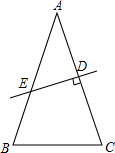 如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB于点E,若AE=BC,则点E是线段AB的黄金分割点吗?说明你的理由.
如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB于点E,若AE=BC,则点E是线段AB的黄金分割点吗?说明你的理由.
分析 连接EC,根据线段垂直平分线的性质得到EA=EC,根据等腰三角形的性质和相似三角形的判定定理证明△CEB∽△ACB,得到$\frac{BE}{BC}$=$\frac{BC}{AB}$,根据黄金分割的概念证明结论.
解答 解:点E是线段AB的黄金分割点.
证明:连接EC,
∵DE是AC的垂直平分线,
∴EA=EC,
又∵AE=BC,
∴EC=BC,
∴∠BEC=∠B,
∵AB=AC,
∴∠ACB=∠B,
∴∠BEC=∠ACB,又∠B=∠B,
∴△CEB∽△ACB,
∴$\frac{BE}{BC}$=$\frac{BC}{AB}$,即BC2=BE•AB,
又∵AE=BC,
∴AE2=BE•AB,即点E是线段AB的黄金分割点.
点评 本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
7.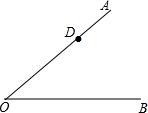 如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
 如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.平面上画出四条直线,交点最多有( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
 已知一次函数y=-$\frac{3}{4}$x+4
已知一次函数y=-$\frac{3}{4}$x+4 如图,将两个同样大小的含30°角的三角板按如图所示的方式放在一起,则∠EDC的度数是105°.
如图,将两个同样大小的含30°角的三角板按如图所示的方式放在一起,则∠EDC的度数是105°.
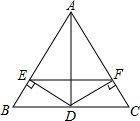 如图,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF,求证:AD垂直平分EF.
如图,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF,求证:AD垂直平分EF.