题目内容
9．
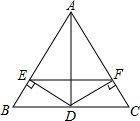如图，DE⊥AB，DF⊥AC，垂足分别为E、F，DE=DF，求证：AD垂直平分EF．
分析 根据直角三角形的判定定理证明Rt△AED≌Rt△AFD，得到AE=AF，根据线段垂直平分线的判定定理证明结论．
解答 解：在Rt△AED和Rt△AFD中，
$\left\{\begin{array}{l}{DE=DF}\\{AD=AD}\end{array}\right.$，
∴Rt△AED≌Rt△AFD，
∴AE=AF，
又∵DE=DF，
∴AD垂直平分EF．
点评 本题考查的是线段垂直平分线的判定和全等三角形的判定和性质，掌握到线段的两个端点的距离相等的点在线段的垂直平分线上是解题的关键．
练习册系列答案
相关题目
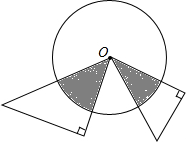一副三角板如图放置，它们的最小锐角顶点与圆心O重合，⊙O的半径是3cm，则图中阴影部分的面积为$\frac{15}{8}$πcm2．（结果保留π）
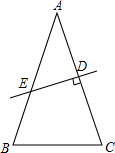如图，在△ABC中，AB=AC，AC的垂直平分线交AC于点D，交AB于点E，若AE=BC，则点E是线段AB的黄金分割点吗？说明你的理由．
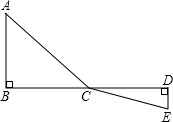如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知AB=3，DE=2，BD=12，设CD=x．