题目内容
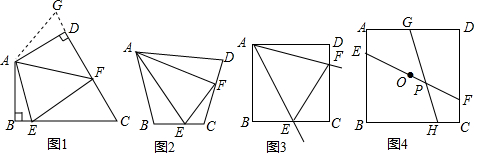
14.“半角型”问题探究:(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE≌△AFG,从而得出结论:EF=BE+DF
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=$\frac{1}{2}$∠BAD,上述结论是否仍然成立,并说明理由.
归纳应用
(3)正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°,已知BE=3,DF=2,求正方形ABCD的边长.
拓展提高
(4)边长为4的正方形ABCD中,点E、F分别在AB、CD上,AE=CF=1,O为EF的中点,动点G、H分别在边AD、BC上,EF与GH的交点P在O、F之间(与0、F不重合),且∠GPE=45°,设AG=m,求m的取值范围.
分析 (1)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(3)延长DC,截取CG=AE,连接BG,根据SAS定理可得出△AEB≌△CGB,故可得出BE=BG,∠ABE=∠CBG,再由∠EBF=45°,∠ABC=90°可得出∠ABE+∠CBF=45°,故∠CBF+∠CBG=45°,由SAS定理可得△EBF≌△GBF,故EF=GF,故△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD,由此可得出结论;
(4)①假设P与O重合,如图4,由O为EF的中点,得到O为正方形ABCD的对称中心,过A作AN∥EF交CD于N,则NF=AE=1,求得DN=CN=2,过O作G′H′∥GH交AD于G′,交BC于H′,于是得到AG′=CH′,DG′=BH′,过A作AM∥G′H′交BC于M,于是得到AG′=MH′,∠MAN=45°,延长CD到Q,使DQ=BM′,由(3)知MN=NQ,设BM=a,则CM=4-a,MN=QN=a+2,根据勾股定理得到AG′=$\frac{4}{3}$;②当H与C重合时,如图5,由①知BM=$\frac{4}{3}$,得到AG″=CM=4-$\frac{4}{3}$=$\frac{8}{3}$;于是得到结论.
解答 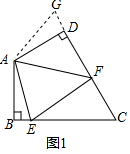 (1)解:如图1,
(1)解:如图1,
在△ABE和△ADG中,
∵$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF;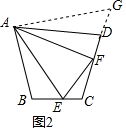
(2)解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,
∵$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AGF(SAS),
∴EF=FG,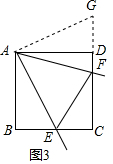
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长CD到点G,截取DG=BE,连接AG,
在△AEB与△AGD中,
∵$\left\{\begin{array}{l}{BE=DG}\\{∠B=∠ADG=90°}\\{AB=AD}\end{array}\right.$,
∴△AEB≌△AGD(SAS),
∴AE=GG,∠BAE=∠GAD,
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAF+∠DAG=45°.
在△EAF与△GAF中,
∵$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△EAF≌△GAF(SAS),
∴EF=GF=BE+DF=5,
设正方形ABCD的边长=x,
∴CE=x-3,CF=x-2,
∵EF2=CE2+CF2,
∴25=(x-3)2+(x-2)2,
∴x=6,x=-1(不合题意,舍去),
∴正方形ABCD的边长是6;
(4)①假设P与O重合,如图4,∵O为EF的中点,
∴O为正方形ABCD的对称中心,
过A作AN∥EF交CD于N,
则NF=AE=1,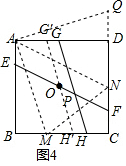
∴DN=CN=2,
过O作G′H′∥GH交AD于G′,交BC于H′,
∴AG′=CH′,DG′=BH′,
过A作AM∥G′H′交BC于M,
∴AG′=MH′,∠G′OE=45°,
∴∠MAN=45°,
延长CD到Q,使DQ=BM′,
由(3)知MN=NQ,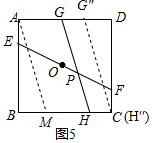
设BM=a,则CM=4-a,MN=QN=a+2,
∵MN2=CM2+CN2,
∴(2+a)2=(4-a)2+22,
解得:a=$\frac{4}{3}$,
∴AG′=$\frac{4}{3}$;
②当H与C重合时,如图5,
由①知BM=$\frac{4}{3}$,
∴AG″=CM=4-$\frac{4}{3}$=$\frac{8}{3}$;
∴m的取值范围为:$\frac{4}{3}$<m≤$\frac{8}{3}$.
点评 本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的性质,锐角三角函数的定义,熟记各性质并作辅助线构造出全等三角形和等腰直角三角形是解题的关键.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案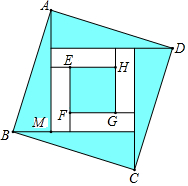 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )| A. | 12S | B. | 10S | C. | 9S | D. | 8S |
| A. | 40% | B. | B56% | C. | 60% | D. | 62% |
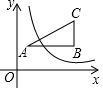 如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )| A. | 1≤k≤4 | B. | 2≤k≤8 | C. | 2≤k≤16 | D. | 8≤k≤16 |
| A. | x<$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
| A. | 平均数是9 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是5 |
| A. | 0.69×10-6 | B. | 6.9×10-7 | C. | 69×10-8 | D. | 6.9×107 |