题目内容
5.(1)分解因式:4x2y-9y;(2)解方程:(2x+3)2=3(2x+3);
(3)解方程:$\frac{x}{x-2}$-$\frac{8}{{x}^{2}-4}$=1.
分析 (1)先提取公因式,再利用公式分解可得;
(2)因式分解法求解可得;
(3)先去分母化分式方程为整式方程,再解整式方程,最后检验可得.
解答 解:(1)原式=y(4x2-9)=y(2x+3)(2x-3);
(2)∵(2x+3)2-3(2x+3)=0,
∴(2x+3)(2x+3-3)=0,即2x(2x+3)=0,
∴x=0或2x+3=0,
解得:x=0或x=-$\frac{3}{2}$;
(3)去分母,得:x(x+2)-8=x2-4,
整理,得:2x-4=0,
解得:x=2,
检验:x=2时,x2-4=0,
∴x=2是原方程的增根,
则原方程无解.
点评 本题主要考查因式分解、解一元二次方程和分式方程,熟练掌握等式的基本性质和解方程的基本步骤是解题的关键.

练习册系列答案
相关题目
16.若α、β是一元二次方程x2+2x-6=0的两个不相等的根,则α2-2β的值是( )
| A. | 10 | B. | 16 | C. | -2 | D. | -10 |
13.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a3)2=a5 | D. | a8÷a2=a4 |
20.-3的倒数是( )
| A. | 3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | ±3 |
15.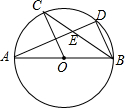 如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )
如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )
 如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )
如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )| A. | AD⊥BD | B. | CB平分∠ABD | C. | BD=2OF | D. | △CEF≌△BED |
 如图,已知AB是⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD=25°.
如图,已知AB是⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD=25°.