Question

如图，在坐标平面内，过点（0，0），（0，3），（3，3），（3，1），（5，1）和（5，0）的水平、竖直连线围成“L”形区域，则过原点且将该图形面积平分的直线与点A、B所在直线的交点的坐标是

 

．

Answer 1

考点：一次函数综合题,矩形的性质,中心对称

专题：

分析：设与AB的交点为M（3，y），延长AB交x轴于点F，则可得矩形BCDF，△OMF及梯形AMOE，根据OM平分该图形面积，可得出S_梯形AEOM=S_矩形BCDF+S_△OMF，得出方程后解出y的值即可得出答案．

解答：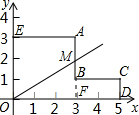
解：设与AB的交点M，坐标为（3，y），
则AM=3-y，MF=y，
故可得S_矩形BCDF=FD×BF=2，S_△OMF=

1

2

OF×MF=

3

2

y，S_梯形AEOM=

1

2

（AM+OE）×AE=

1

2

（3-y+3）×3=9-

3

2

y，
∵OM平分该图形面积，
∴S_梯形AEOM=S_矩形BCDF+S_△OMF，即9-

3

2

y=2+

3

2

y，
解得：y=

7

3

，
故可得点M的坐标为（3，

7

3

）．
故答案为：（3，

7

3

）．

点评：此题考查了一次函数综合题，涉及了矩形的性质、梯形的面积，解答本题的关键是设出交点的坐标，然后利用面积相等建立方程，难度较大，注意所学知识的融会贯通．