题目内容
9.若一次函数y=(2-m)x+m的图象经过第一、二、四象限时,m的取值范围是m>2,若它的图象不经过第二象限,m的取值范围是m≤0.分析 根据图象在坐标平面内的位置关系确定m的取值范围,从而求解;
根据函数的解析式可知,一次函数的斜率大于0,则函数必过一、三象限;如果函数图象不过第二象限,则函数必交y轴于负半轴(或原点),即m-2≤0,由此可求得m的取值范围.
解答 解:由一次函数y=(2-m)x+m的图象经过第一、二、四象限,
可得函数y随x的增大而减小,与y轴交于正半轴,
∴2-m<0,且m>0,
则m的取值范围是m>2;
一次函数y=(2-m)x+m的图象不经过第二象限,
则m≤0,解得m≤0,
故答案为:m>2,m≤0.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.按下列程序计算,把答案写在表格内:
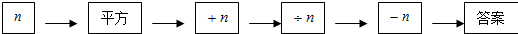
(1)填写表格:
(2)请将题中计算程序用代数式表达出来,并化简.
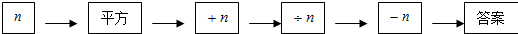
(1)填写表格:
| 输入n | 3 | $\frac{1}{2}$ | -2 | … |
| 输出答案 | 1 | 1 | 1 | … |
1.已知关于x的方程-4x+2k=10的解是x=k-1,则|k|的值是( )
| A. | -3 | B. | -7 | C. | 3 | D. | 7 |
19.下列四个图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,数轴上有两点A、B,如果点A表示的数是-3,线段AB=7,那么点B表示的数是4或-10.
如图,数轴上有两点A、B,如果点A表示的数是-3,线段AB=7,那么点B表示的数是4或-10.