Question

16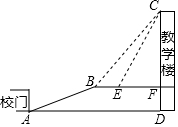．某山区为改善办学条件，依山新建一座教学楼，校门A处，有一坡度i=5：12的斜坡AB，在坡顶B处（铅直高度为10米）看教学楼CF的楼顶C的仰角∠CBF=53°，在E处仰角C的仰角∠CEF=63.4°，按规划要在离B点6米远的E处建一悬挂国旗的旗杆．
（1）求斜坡AB的长度；
（2）求旗杆处离教学楼的距离．
（参考数据：tan63.4°≈2，tan53°≈$\frac{4}{3}$）

Answer 1

分析 （1）作BG⊥AD，由BG=10、i=$\frac{BG}{AG}=\frac{5}{12}$得AG=24，根据勾股定理求解可得；
（2）设EF=x米，则BF=6+x（米），由CF=BFtan∠CBF=EFtan∠CEF得出关于x的方程，解之可得．

解答 解：（1）如图，过点B作BG⊥AD于点G，

则BG=10，
∵i=$\frac{BG}{AG}=\frac{5}{12}$，
∴AG=24，
则AB=$\sqrt{A{G}^{2}+B{G}^{2}}$=$\sqrt{1{0}^{2}+2{4}^{2}}$=26，
答：斜坡AB的长度为26米；

（2）设EF=x米，则BF=6+x（米），
∵在Rt△BCF中，CF=BFtan∠CBF=（6+x）tan53°，
在Rt△ECF中，CF=EFtan∠CEF=tan63.4°x，
∴（6+x）tan53°=tan63.4°x，
解得：x=$\frac{6•tan53°}{tan63.4°-tan53°}$≈12，
答：旗杆处离教学楼的距离约为12米．

点评 本题考查了解直角三角形的应用-仰角和俯角问题，解直角三角形的应用-坡度和坡比问题，正确理解题意是解题的关键．