题目内容
1. 如图,在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将其沿AE翻折后,点B恰好与点C重合,则折痕AE的长为3.
如图,在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将其沿AE翻折后,点B恰好与点C重合,则折痕AE的长为3.
分析 首先由翻折性质得出AE是BC的垂直平分线,点E是BC的中点,则BE=2,根据勾股定理计算即可.
解答 解:由折叠得:AE是BC的垂直平分线,
∵四边形ABCD是平行四边形,
∴BC=AD=4,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2,
由勾股定理得:AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{(\sqrt{13})^{2}-{2}^{2}}$=3,
则折痕AE的长为3.
故答案为:3.
点评 本题考查了平行四边形的性质和翻折变换,熟练掌握平行四边形的对边相等且平行;明确翻折变换(折叠问题)实质上就是轴对称变换;它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,本题沿AE翻折,则直线AE就是对称轴.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
11.受今年五月份雷暴雨影响,深圳某路段长120米的铁路被水冲垮了,施工队抢分夺秒每小时比原计划多修5米,结果提前4小时开通了列车.若原计划每小时修x米,则所列方程正确的是( )
| A. | $\frac{120}{x}$-$\frac{120}{x+5}$=4 | B. | $\frac{120}{x+5}$-$\frac{120}{x}$=4 | C. | $\frac{120}{x-5}$-$\frac{120}{x}$=4 | D. | $\frac{120}{x}$-$\frac{120}{x-5}$=4 |
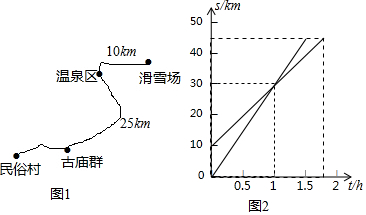
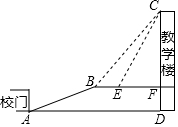 某山区为改善办学条件,依山新建一座教学楼,校门A处,有一坡度i=5:12的斜坡AB,在坡顶B处(铅直高度为10米)看教学楼CF的楼顶C的仰角∠CBF=53°,在E处仰角C的仰角∠CEF=63.4°,按规划要在离B点6米远的E处建一悬挂国旗的旗杆.
某山区为改善办学条件,依山新建一座教学楼,校门A处,有一坡度i=5:12的斜坡AB,在坡顶B处(铅直高度为10米)看教学楼CF的楼顶C的仰角∠CBF=53°,在E处仰角C的仰角∠CEF=63.4°,按规划要在离B点6米远的E处建一悬挂国旗的旗杆.
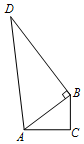 某机器零件呈四边形ACBD的形状,要求∠ABD=90°,∠C=90°.现测得∠ABD=90°,AD=39,BD=36,AC=12,BC=9.你认为这个零件合格吗?说明理由.
某机器零件呈四边形ACBD的形状,要求∠ABD=90°,∠C=90°.现测得∠ABD=90°,AD=39,BD=36,AC=12,BC=9.你认为这个零件合格吗?说明理由.