题目内容
8.市园林处为了对一段公路进行绿化,计划购买A,B两种风景树共900棵.A,B两种树的相关信息如表:| 品种项目 | 单价(元/棵) | 成活率 |
| A | 80 | 92% |
| B | 100 | 98% |
(1)求y与x之间的函数关系式.
(2)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?此时最低费用为多少?
分析 (1)根据购树的总费用=买A种树的费用+买B种树的费用,化简后便可得出y与x的函数关系式;
(2)先根据A种树成活的数量+B种树成活的数量≥树的总量×平均成活率,列出不等式,得出x的取值范围,然后根据一次函数的性质判断出最佳的方案.
解答 解:(1)由题意,得:y=80x+100(900-x)
化简,得:y=-20x+90000(0≤x≤900且为整数);
(2)由题意得:92%x+98%(900-x)≥94%×900,
解得:x≤600.
∵y=-20x+90000随x的增大而减小,
∴当x=600时,购树费用最低为y=-20×600+90000=78000.
当x=600时,900-x=300,
故此时应购A种树600棵,B种树300棵,最低费用为78000元.
点评 本题考查了一次函数的应用,一元一次不等式的应用,一次函数的性质,利用成活率得到自变量的取值范围是解决本题的难点.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.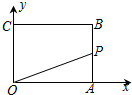 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 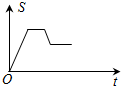 | D. | 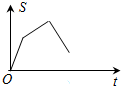 |
20.若函数y=$\frac{k-3}{x}$的图象在其所在的每一象限内,y随x的增大而增大,则k的取值范围是( )
| A. | k>3 | B. | k<3 | C. | k>-3 | D. | k<-3 |
 如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB'C'的位置,连接CC',若CC'∥AB,则旋转角α的度数为40°.
如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB'C'的位置,连接CC',若CC'∥AB,则旋转角α的度数为40°.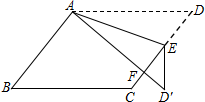 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.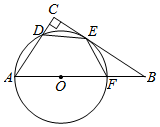 如图,在Rt△ABC中,∠C=90°,点D、E、F分别在AC、BC、AB边上,以AF为直径的⊙O恰好经过D、E,且DE=EF.
如图,在Rt△ABC中,∠C=90°,点D、E、F分别在AC、BC、AB边上,以AF为直径的⊙O恰好经过D、E,且DE=EF.