题目内容
20．下列说法中正确的是（ ）| A． | x2+y是整式 | B． | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C． | 单项式$-\frac{2}{3}{a^2}b$的系数为-2 | D． | $\frac{1}{a}$和0都是单项式 |
分析 根据整式的定义判断A；根据多项式的次数的定义判断B；根据单项式的系数的定义判断C；根据单项式的定义判断D．
解答 解：A、x2+y是整式，故本选项正确；
B、多项式-3a2b+7a2b2+1的次数是4，故本选项错误；
C、单项式$-\frac{2}{3}{a^2}b$的系数为-$\frac{2}{3}$，故本选项错误；
D、$\frac{1}{a}$不是单项式，0是单项式，故本选项错误；
故选A．
点评 本题考查了单项式、单项式的系数、多项式的次数以及整式的定义：数或字母的积组成的式子叫做单项式，单独的一个数或字母也是单项式，单项式中的数字因数叫做单项式的系数；几个单项式的和叫做多项式，每个单项式叫做多项式的项，其中不含字母的项叫做常数项，多项式中次数最高的项的次数叫做多项式的次数；单项式和多项式统称为整式．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
16．下列几何体中，主视图和左视图都是矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
11．下列说法正确的是（ ）
| A． | 4的平方根是2 | B． | 1的立方根是±1 | ||
| C． | $\sqrt{4}$的算术平方根是2 | D． | -1的立方根是-1 |
8．下列运算中正确的是（ ）
| A． | 3a+2a=5a2 | B． | -x2•（-x）3=（-x）5 | C． | 2a2•a3=2a6 | D． | （a-b）（b-a）=-（a-b）2 |
15．下列为二次根式的是（ ）
①$\sqrt{3}$，②$\sqrt{x}$（x＞0），③$\sqrt{a}$，④$\sqrt{4}$-2，⑤$\sqrt{-4}$-2．
①$\sqrt{3}$，②$\sqrt{x}$（x＞0），③$\sqrt{a}$，④$\sqrt{4}$-2，⑤$\sqrt{-4}$-2．
| A． | ①②③ | B． | ①②④ | C． | ②③⑤ | D． | ③④⑤ |
5．下列说法中错误的是（ ）
| A． | 4的算术平方根是2 | B． | 负数有立方根，并且是负数 | ||
| C． | 8的立方根是±2 | D． | -1的立方根是-1 |
12．数学问题：在1～51这51个自然数中，每次取两个不同的数，使得所取的两个数之和大于51，有多少中不同取法？
数学模型：为找到解决上面问题的方法，先建立简单的数学模型进行研究：
（1）在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，有多少种不同取法？
解决问题过程如下：
第1行有1种取法（1，5）
第2行有2种取法（2，4），（2，5）
第3行有3种取法（3，3），（3，4），（3，5）
第4行有4种取法（4，2），（4，3），（4，4），（4，5）
第5行有5种取法（5，1），（5，2），（5，3），（5，4），（5，5）
共有1+2+3+4+5种取法，因为每次取两个不同的数，所以在这些取法中不包括（3，3），（4，4），（5，5），要从总数中减去这3中取法，并且（4，2）与（2，4），（4，3）与（3，4），（5，1）与（1，5），（5，2）与（2，5），…（5，4）与（4，5）是同一种取法，因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法．
（2）在1～6这6个自然数中，每次取两个不同的数，使得所取的两个数之和大于6，有多少种不同的取法？
解决问题过程如下：
第1行有1种取法（1，6）
第2行有2种取法（2，5），（2，6）
第3行有3种取法（3，4），（3，5），（3，6）
第4行有4种取法（4，3），（4，4），（4，5），（4，6）
第5行有5种取法（5，2），（5，3），（5，4），（5，5），（5，6）
第6行有6种取法（6，1），（6，2），（6，3），6，4），（6，5），（6，6）
共有1+2+3+4+5+6种取法，因为每次取两个不同的数，所以在这些取法中不包括（4，4），（5，5），（6，6），要从总数中减去这3中取法，并且（4，3）与（3，4），（5，2）与（2，5），（5，3）与（3，5），（5，4）与（4，5），（6，1）与（1，6），（6，2）与（2，6）…（6，5）与（5，6）是同一种取法，因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法．
归纳探究：
仿照上述研究问题的思路和解决过程，回答下列提出的问题：
（1）在1～7这7个自然数中，每次取两个不同的数，使得所取的两个数之和大于7，共有12种不同取法．（只填结果）
（2）在1～8这8个自然数中，每次取两个不同的数，使得所取的两个数之和大于8，共有16种不同取法．（只填结果）
（3）在1～n（n为奇数）这n个自然数中，每次取两个不同的数，使得所取的两个数之和大于n，共有$\frac{{n}^{2}-1}{4}$种不同取法．（只填最简算式）
（4）在1～n（n为偶数）这n个自然数中，每次取两个不同的数，使得所取的两个数之和大于n，共有$\frac{{n}^{2}}{4}$种不同取法．（只填最简算式）
类比应用：类比上述研究方法或应用其结论，解决下列提出的问题：
（5）各边长都是整数，最大边长为51的三角形有多少个？（直接列出算术，并计算结果）
数学模型：为找到解决上面问题的方法，先建立简单的数学模型进行研究：
（1）在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，有多少种不同取法？
解决问题过程如下：
| 1 | 2 | 3 | 4 | 5 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） |
第2行有2种取法（2，4），（2，5）
第3行有3种取法（3，3），（3，4），（3，5）
第4行有4种取法（4，2），（4，3），（4，4），（4，5）
第5行有5种取法（5，1），（5，2），（5，3），（5，4），（5，5）
共有1+2+3+4+5种取法，因为每次取两个不同的数，所以在这些取法中不包括（3，3），（4，4），（5，5），要从总数中减去这3中取法，并且（4，2）与（2，4），（4，3）与（3，4），（5，1）与（1，5），（5，2）与（2，5），…（5，4）与（4，5）是同一种取法，因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法．
（2）在1～6这6个自然数中，每次取两个不同的数，使得所取的两个数之和大于6，有多少种不同的取法？
解决问题过程如下：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
第2行有2种取法（2，5），（2，6）
第3行有3种取法（3，4），（3，5），（3，6）
第4行有4种取法（4，3），（4，4），（4，5），（4，6）
第5行有5种取法（5，2），（5，3），（5，4），（5，5），（5，6）
第6行有6种取法（6，1），（6，2），（6，3），6，4），（6，5），（6，6）
共有1+2+3+4+5+6种取法，因为每次取两个不同的数，所以在这些取法中不包括（4，4），（5，5），（6，6），要从总数中减去这3中取法，并且（4，3）与（3，4），（5，2）与（2，5），（5，3）与（3，5），（5，4）与（4，5），（6，1）与（1，6），（6，2）与（2，6）…（6，5）与（5，6）是同一种取法，因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法．
归纳探究：
仿照上述研究问题的思路和解决过程，回答下列提出的问题：
（1）在1～7这7个自然数中，每次取两个不同的数，使得所取的两个数之和大于7，共有12种不同取法．（只填结果）
（2）在1～8这8个自然数中，每次取两个不同的数，使得所取的两个数之和大于8，共有16种不同取法．（只填结果）
（3）在1～n（n为奇数）这n个自然数中，每次取两个不同的数，使得所取的两个数之和大于n，共有$\frac{{n}^{2}-1}{4}$种不同取法．（只填最简算式）
（4）在1～n（n为偶数）这n个自然数中，每次取两个不同的数，使得所取的两个数之和大于n，共有$\frac{{n}^{2}}{4}$种不同取法．（只填最简算式）
类比应用：类比上述研究方法或应用其结论，解决下列提出的问题：
（5）各边长都是整数，最大边长为51的三角形有多少个？（直接列出算术，并计算结果）
9．
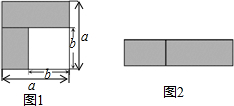通过计算几何图形的面积可表示代数恒等式，图中可表示的代数恒等式是（ ）
通过计算几何图形的面积可表示代数恒等式，图中可表示的代数恒等式是（ ）| A． | （a-b）2=a2-2ab+b2 | B． | （a+b）2=a2+2ab+b2 | C． | 2a（a+b）=2a2+2ab | D． | （a+b）（a-b）=a2-b2 |