题目内容
9．
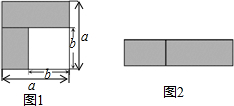通过计算几何图形的面积可表示代数恒等式，图中可表示的代数恒等式是（ ）| A． | （a-b）2=a2-2ab+b2 | B． | （a+b）2=a2+2ab+b2 | C． | 2a（a+b）=2a2+2ab | D． | （a+b）（a-b）=a2-b2 |
分析 根据阴影部分面积的两种表示方法，即可解答．
解答 解：图1中阴影部分的面积为：a2-b2，
图2中的面积为：（a+b）（a-b），
则（a+b）（a-b）=a2-b2，
故选：D．
点评 本题考查了平方差公式的几何背景，解决本题的关键是表示阴影部分的面积．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
如图，在平面直角坐标系中，已知点A（1，0），B（3，2），请在图中画出线段AB，并在y轴上找一点P，使得PA=PB．（要求：尺规作图，并保留作图痕迹）
20．下列说法中正确的是（ ）
| A． | x2+y是整式 | B． | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C． | 单项式$-\frac{2}{3}{a^2}b$的系数为-2 | D． | $\frac{1}{a}$和0都是单项式 |
17．下列各式中，正确的是（ ）
| A． | $\sqrt{16}$=±4 | B． | $\root{3}{8}$=±2 | C． | （-$\sqrt{2}$）4=-4 | D． | （$\root{5}{-8}$）5=-8 |
4．下列结论正确的是（ ）
| A． | 2-1=-2 | |
| B． | 单项式-x2的系数是-1 | |
| C． | 使式子$\sqrt{x-2}$有意义的x的取值范围是x＜2 | |
| D． | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0，则a=-1 |
14．下列说法正确的是（ ）
| A． | -$\frac{2}{5}$是$\sqrt{\frac{4}{25}}$的平方根 | B． | -$\frac{2}{5}$是$\frac{4}{25}$的平方根 | ||
| C． | $\frac{4}{25}$的平方根是-$\frac{2}{5}$ | D． | $\sqrt{\frac{4}{25}}$的平方根是±$\frac{2}{5}$ |
1．下列各式中，一定是二次根式的是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{-10}$ | C． | $\sqrt{a+1}$ | D． | $\sqrt{a}$ |
18．下列各式中一定正确的是（ ）
| A． | （2x-3）0=1 | B． | π0=0 | C． | （a2-1）0=1 | D． | （m2+1）0=1 |