题目内容
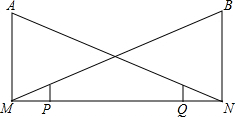 如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.
如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.(1)求证:AM=BN;
(2)求两个路灯之间的距离;
(3)当王军走到路灯B时,他在路灯A下的影长是多少?
考点:相似三角形的应用,中心投影
专题:应用题
分析:(1)如图,由PE∥BN可判断△MPE∽△MNB,利用相似比可得到BN=
;同理可得AM=
,利用PE=QF,MP=NQ即可得到AM=BN;
(2)由(1)中
=
,即
=
,得到x=
MN,再根据MP+PQ+NQ=MN得到
MN+12+
MN=MN,然后解关于MN的一次方程即可;
(3)解:如图,AM=9.6m,MN=18m,NG=1.6m,利用NG∥AM得到△KNG∽△KMA,利用相似比可计算出KM的长.
| PE•MN |
| MP |
| FQ•MN |
| NQ |
(2)由(1)中
| FQ |
| AM |
| NQ |
| NM |
| 1.6 |
| 9.6 |
| x |
| MN |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
(3)解:如图,AM=9.6m,MN=18m,NG=1.6m,利用NG∥AM得到△KNG∽△KMA,利用相似比可计算出KM的长.
解答:(1)证明:如图,
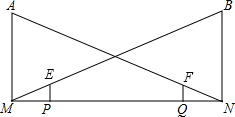
∵PE∥BN,
∴△MPE∽△MNB,
∴
=
,
∴BN=
;
∵QF∥AM,
∴△NQF∽△NMA,
∴
=
,
∴AM=
,
而PE=QF,MP=NQ,
∴AM=BN;
(2)解:∵
=
,即
=
,
∴x=
MN,
而MP+PQ+NQ=MN,
∴
MN+12+
MN=MN,
∴MN=18(m);
(3)解:如图,AM=9.6m,MN=18m,NG=1.6m,
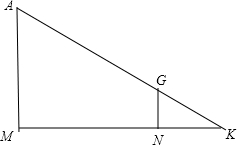
∵NG∥AM,
∴△KNG∽△KMA,
∴
=
,即
=
,
∴KN=3.6(m),
即当王军走到路灯B时,他在路灯A下的影长是3.6m.

∵PE∥BN,
∴△MPE∽△MNB,
∴
| PE |
| BN |
| MP |
| MN |
∴BN=
| PE•MN |
| MP |
∵QF∥AM,
∴△NQF∽△NMA,
∴
| FQ |
| AM |
| NQ |
| NM |
∴AM=
| FQ•MN |
| NQ |
而PE=QF,MP=NQ,
∴AM=BN;
(2)解:∵
| FQ |
| AM |
| NQ |
| NM |
| 1.6 |
| 9.6 |
| x |
| MN |
∴x=
| 1 |
| 6 |
而MP+PQ+NQ=MN,
∴
| 1 |
| 6 |
| 1 |
| 6 |
∴MN=18(m);
(3)解:如图,AM=9.6m,MN=18m,NG=1.6m,

∵NG∥AM,
∴△KNG∽△KMA,
∴
| NG |
| AM |
| KN |
| KM |
| 1.6 |
| 9.6 |
| KN |
| KN+18 |
∴KN=3.6(m),
即当王军走到路灯B时,他在路灯A下的影长是3.6m.
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.

练习册系列答案
相关题目
 如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么?
如图,BD、CE是△ABC的高,△ADE与△ABC相似吗?为什么? 如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.
如图,在△ABC中,AB=AC,D是AC上一点,过D作DE⊥BC于E,与BA的延长线交于F,求证:AD=AF.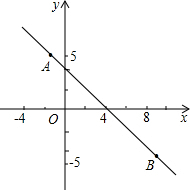 如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到,
如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到, 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长. 如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
如图,在梯形ABCD中,AB∥CD,AD=BC,延长AB到E,使BE=DC.试判断AC与CE的大小关系?并说明理由.
 如图,在四边形ABCD中,已知E是对角线AC上的点.EF∥BC,EG∥CD,E,G分别在AB,AD上,EF=10,BC=14,AG=15.求AD的长.
如图,在四边形ABCD中,已知E是对角线AC上的点.EF∥BC,EG∥CD,E,G分别在AB,AD上,EF=10,BC=14,AG=15.求AD的长.