题目内容
11.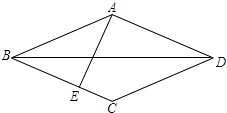 已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=$\frac{1}{2}$,则AB=$\sqrt{5}$,sin∠ABE=$\frac{4}{5}$.
已知:如图,在菱形ABCD中,AE⊥BC,垂足为E,对角线BD=4,tan∠CBD=$\frac{1}{2}$,则AB=$\sqrt{5}$,sin∠ABE=$\frac{4}{5}$.
分析 (1)首先连接AC,AC与BD相交于点O,由四边形ABCD是菱形,可得AC⊥BD,BO=$\frac{1}{2}$BD=2,又由tan∠CBD=$\frac{1}{2}$,可求得OC的长,然后由勾股定理求得边AB的长;
(2)由AE⊥BC,利用S菱形ABCD=BC•AE=$\frac{1}{2}$BD•AC,即可求得AE的长,继而求得∠ABE的正弦值.
解答  解:(1)连接AC,AC与BD相交于点O,
解:(1)连接AC,AC与BD相交于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,BO=$\frac{1}{2}$BD=2,
∵Rt△BOC中,tan∠CBD=$\frac{OC}{OB}$=,
∴OC=1,
∴AB=BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$;
(2)∵AE⊥BC,
∴S菱形ABCD=BC•AE=$\frac{1}{2}$BD•AC,
∵AC=2OC=2,
∴$\sqrt{5}$AE=$\frac{1}{2}$×2×4,
∴AE=$\frac{4\sqrt{5}}{5}$,
∴sin∠ABE=$\frac{AE}{AB}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 此题考查了菱形的性质、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是( )
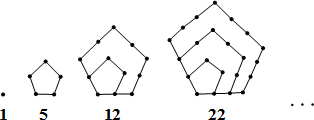

| A. | 62 | B. | 70 | C. | 84 | D. | 108 |
2.-4.5×10-5表示( )
| A. | -000045 | B. | -0.000045 | C. | -450000 | D. | -45000 |
6.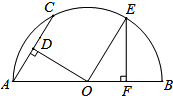 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{6}$ | B. | x6÷x3=x2 | C. | $\sqrt{4}$=2 | D. | a2(-a2)=a4 |
3.2015年,永州市政府工作报告指出,要大力发展现代农业,做强优势产业,确保粮食面积825万亩,水果150万亩,蔬菜230万亩,烤烟25万亩.其中粮食面积825万亩中的“825万”用科学记数法表示为( )
| A. | 8.25×107 | B. | 8.25×106 | C. | 82.5×105 | D. | 0.825×107 |
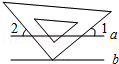 如图,已知a∥b,把三角板的直角顶点放在直线b上,若∠1=32°18′,则∠2的度数为57°42′.
如图,已知a∥b,把三角板的直角顶点放在直线b上,若∠1=32°18′,则∠2的度数为57°42′.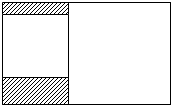 如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积.
如图所示,某工人师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m.求裁剪后剩下的阴影部分的面积.