题目内容
16.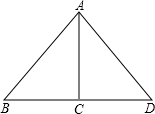 我们把两个三角形的外心之间的距离叫做外心距.如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90°,点D在边BC的延长线上,如果BC=DC=3,那么△ABC和△ACD的外心距是3.
我们把两个三角形的外心之间的距离叫做外心距.如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90°,点D在边BC的延长线上,如果BC=DC=3,那么△ABC和△ACD的外心距是3.
分析 利用直角三角形的性质得出两三角形的外心距为△ABD的中位线,即可得出答案.
解答 解:∵∠ACB=∠ACD=90°,
∴Rt△ABC和Rt△ACD分别是AB,AD的中点,
∴两三角形的外心距为△ABD的中位线,即为$\frac{1}{2}$BD=3.
故答案为:3.
点评 此题主要考查了三角形的外心,得出外心的位置是解题关键.

练习册系列答案
相关题目
6.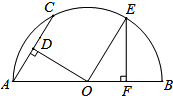 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F,若AC=4,则OF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
7.能说明命题“关于x的一元二次方程x2+mx+4=0,当m<-2时必有实数解”是假命题的一个反例为( )
| A. | m=-4 | B. | m=-3 | C. | m=-2 | D. | m=4 |
5.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(-m,0)在( )
| A. | x轴正半轴上 | B. | y轴正半轴上 | C. | x轴负半轴上 | D. | y轴负半轴上 |

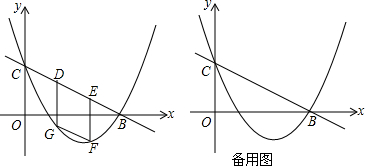
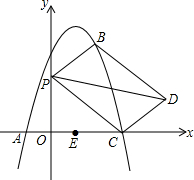 如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD.
如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD. 如图,已知∠1=∠2,∠3+∠4=180°,试探究AB与EF的位置关系,并说明理由.
如图,已知∠1=∠2,∠3+∠4=180°,试探究AB与EF的位置关系,并说明理由.