题目内容
20.已知正方形ABCD,在这个正方形所在的平面内有一点P,若点P到AB的距离是1,点P到BC的距离是2,点P到CD的距离是4,则点P到DA的距离是1或3或5或7.分析 利用两平行直线之间的距离可作作11∥AB,l2∥AB,且11和l2到AB的距离为1,作13∥BC,l4∥BC,且13和l4到BC的距离为2,如图,讨论:若P1F=4,则HF=4+1=5,所以MQ=AB=BC=HF=5,于是得到P1M=MQ-P1Q=3;同理可得P3M=7;若P2F=4,则HF=3,所以EN=AB=BC=HF=3,则P2E=EN-P2N=3-2=1;同理可得P4E=5.
解答 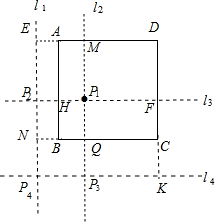 解:如图,作11∥AB,l2∥AB,且11和l2到AB的距离为1,作13∥BC,l4∥BC,且13和l4到BC的距离为2,4条直线相交于P1,P2,P3,P4,
解:如图,作11∥AB,l2∥AB,且11和l2到AB的距离为1,作13∥BC,l4∥BC,且13和l4到BC的距离为2,4条直线相交于P1,P2,P3,P4,
若12到CD的距离为4,则P1F=4,
∵P1H=1,P1Q=2,
∴HF=4+1=5,
∵四边形ABCD为正方形,
∴MQ=AB=BC=HF=5,
∴P1M=MQ-P1Q=5-2=3;
同理可得P3M=7,
若11到CD的距离为4,则P2F=4,
∵P2H=1,P1N=2,
∴HF=4-1=3,
∵四边形ABCD为正方形,
∴EN=AB=BC=HF=3,
∴P2E=EN-P2N=3-2=1;
同理可得P4E=5,
综上所述,点P到DA的距离为1或3或5或7.
故答案为1或3或5或7.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了分类讨论思想的应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5.某人出去散步,从家里出发,走了20min,到达一个离家900m的阅报亭,看了10min报纸后,用了15min返回家里,下面图象中正确表示此人离家的距离y(m)与时间x(min)之家关系的是( )
| A. | 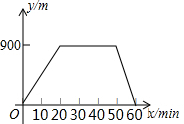 | B. | 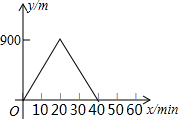 | ||
| C. | 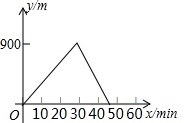 | D. | 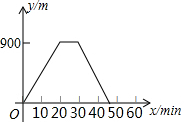 |
12.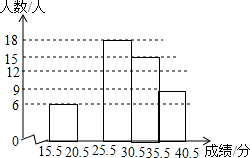 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
请结合图表信息解答下列问题:
(1)a=12,b=0.25;
(2)补全频数分布直方图;
(3)该问题中的样本容量是多少?答:60;
(4)如果成绩在30分以上(不含30分)的同学属于优良,请你估计该校八年级约有多少人达到优良水平?
 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).| 分组 | 频数 | 频率 |
| 15.5~20.5 | 6 | 0.10 |
| 20.5~25.5 | a | 0.20 |
| 25.5~30.5 | 18 | 0.30 |
| 30.5~35.5 | 15 | b |
| 35.5~40.5 | 9 | 0.15 |
(1)a=12,b=0.25;
(2)补全频数分布直方图;
(3)该问题中的样本容量是多少?答:60;
(4)如果成绩在30分以上(不含30分)的同学属于优良,请你估计该校八年级约有多少人达到优良水平?
9.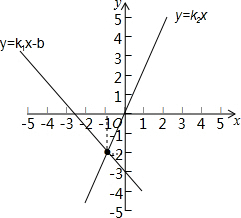 直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
 直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y-=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式组0>k2x>k1x+b的解集为( )| A. | x>-1 | B. | -1<x<0 | C. | -2<x<-1 | D. | -2<x<0 |
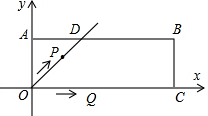 在直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
在直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.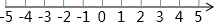 解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.
解不等式组:$\left\{\begin{array}{l}{2(x-1)≥x-4}\\{\frac{x+7}{2}>x+2}\end{array}\right.$,并把不等式组的解集表示在数轴上.