题目内容
5.(1)如图(1),已知△ABC为等边三角形,以BC为直径的⊙O交AB,AC于点D,求∠DOE的度数;(2)如图(2),在ABC中,若∠A=60°,以BC为直径作圆交AB、AC分别于点D、E.探求∠DOE是否为定值?若是定值求其值;若不是,请说明理由.
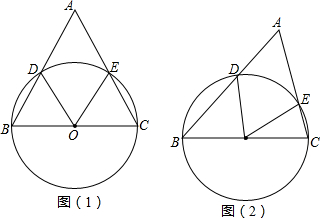
分析 (1)根据等边三角形的性质证得∠B=∠C=60°,进而证得△OBD和△OEC都是等边三角形,得出∠BOD=∠COE=60°,从而求得∠DOE=60°;
(2)构造∠DOE所对的弧所对的圆周角,只要求得圆周角是30°即可.
解答  解:(1)∵△BAC是等边三角形,
解:(1)∵△BAC是等边三角形,
∴∠B=∠C=60°.
∵OD=OB=OE=OC,
∴△OBD和△OEC都是等边三角形.
∴∠BOD=∠COE=60°.
∴∠DOE=60°.
(2)结论(1)仍成立.
证明:如图连接CD,
∵BC是直径,
∴∠BDC=90°.
∴∠ADC=90°.
∵∠A=60°,
∴∠ACD=30°.
∴∠DOE=2∠ACD=60°.
点评 本题考查了等边三角形的性质,圆周角定理,解答本题的关键是能够熟练运用圆周角定理及其推论求得有关角的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )| A. | △ABC≌△AFE | B. | △AFE≌△ADC | C. | △AFE≌△DFC | D. | △ABC≌△AED |
15.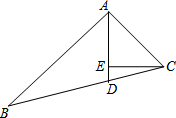 如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
 如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )| A. | 2∠ACE=∠B+∠ECD | B. | ∠ACE=∠B+∠ECD | C. | ∠ACE=∠B+2∠ECD | D. | ∠ACE=2(∠B+∠ECD) |
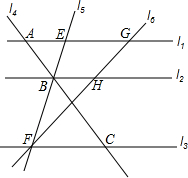 如图,已知,直线l1,l2,l3依次截直线l4于点A、B、C,截直线l5于点E、B、F,截直线l6于点G、H、F,且l1∥l2∥l3,BE=2,BF=4,AB=2.5,FG=9.求BC、FH、GH的长.
如图,已知,直线l1,l2,l3依次截直线l4于点A、B、C,截直线l5于点E、B、F,截直线l6于点G、H、F,且l1∥l2∥l3,BE=2,BF=4,AB=2.5,FG=9.求BC、FH、GH的长.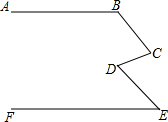 如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数.
如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数.