题目内容
在Rt△ABC中AB的长度为3cm,AC的长度为4cm,BC的长度是多少才能构成面积最大的直角三角形( )
| A、5cm | ||
B、
| ||
C、5cm或
| ||
| D、6cm |
考点:勾股定理的逆定理
专题:
分析:由于Rt△ABC中没有明确哪个角是直角,那么BC可以是斜边,也可以是直角边,根据直角三角形中斜边最长可知BC是斜边时,△ABC的面积最大,利用勾股定理求出BC的长度即可.
解答:解:∵Rt△ABC中AB的长度为3cm,AC的长度为4cm,
∴BC是斜边时,△ABC的面积最大,
此时BC=
=5cm.
故选A.
∴BC是斜边时,△ABC的面积最大,
此时BC=
| AB2+AC2 |
故选A.
点评:本题考查了勾股定理,根据条件得出BC是斜边时,△ABC的面积最大是解题的关键.

练习册系列答案
相关题目
 如图是一家商场某品牌运动鞋不同码数的销售情况,你认为这家商场进货最多的运动鞋的码数会是( )
如图是一家商场某品牌运动鞋不同码数的销售情况,你认为这家商场进货最多的运动鞋的码数会是( )| A、40 | B、41 | C、42 | D、43 |
一元二次方程2x2-bx=1的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
将抛物线y=2x2向左平移2个单位后所得到的抛物线为( )
| A、y=2x2-2 |
| B、y=2x2+2 |
| C、y=2(x-2)2 |
| D、y=2(x+2)2 |
观察下列数据:①7、24、25,②7、12、15,③12,15,20,④8,15,17.其中能作为直角三角形三边长的有( )
| A、1组 | B、2组 | C、3组 | D、4组 |
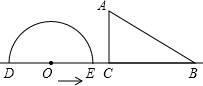 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为 如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.
如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.