题目内容
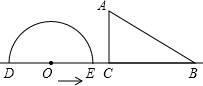 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为考点:切线的性质,扇形面积的计算
专题:动点型
分析:本题要分当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形分别计算.
解答: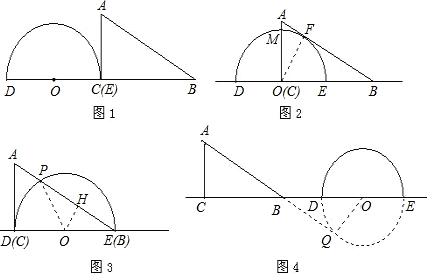 解:当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
解:当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=
π×62=9π(cm2)
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
则OH=3cm,BH=3
cm,BP=6
cm,S△POB=
×6
×3=9
(cm2)
又因为∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重叠部分面积为:S△POB+S扇形DOP=9
+6π(cm2),
故答案为:9π或9
+6π.
 解:当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.
解:当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有图2与图3所示的两种情形.①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:S扇形EOM=
| 1 |
| 4 |
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
则OH=3cm,BH=3
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
又因为∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重叠部分面积为:S△POB+S扇形DOP=9
| 3 |
故答案为:9π或9
| 3 |
点评:本题主要考查了切线的性质和扇形面积的计算,切线的性质:①圆的切线垂直于经过切点的半径;②经过圆心且垂直于切线的直线必经过切点;③经过切点且垂直于切线的直线必经过圆心.

练习册系列答案
相关题目
在Rt△ABC中AB的长度为3cm,AC的长度为4cm,BC的长度是多少才能构成面积最大的直角三角形( )
| A、5cm | ||
B、
| ||
C、5cm或
| ||
| D、6cm |
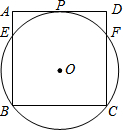 如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则
如图,正方形ABCD的边AD与⊙O相切于点P,E、F是正方形与圆的另两个交点.若BC=4,则