题目内容
16.先化简,再求值:$\frac{2}{x+1}$-$\frac{x-2}{{x}^{2}-1}$,其中x=4cos60°+1.分析 先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{2}{x+1}$-$\frac{x-2}{{x}^{2}-1}$
=$\frac{2(x-1)-(x-2)}{(x+1)(x-1)}$
=$\frac{2x-2-x+2}{(x+1)(x-1)}$
=$\frac{x}{(x+1)(x-1)}$
=$\frac{x}{{x}^{2}-1}$,
当x=4cos60°+1=4×$\frac{1}{2}$+1=2+1=3时,原式=$\frac{3}{{3}^{2}-1}=\frac{3}{8}$.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
 如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
 如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20.
如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20.
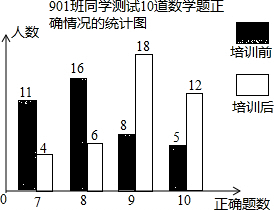 小潘老师为了检测901班同学培训效果做了一项教学实验:通过测试10道数学题了解培训前和培训后学生的解题情况.并绘成如下的条形统计图.根据统计图,回答下列问题:
小潘老师为了检测901班同学培训效果做了一项教学实验:通过测试10道数学题了解培训前和培训后学生的解题情况.并绘成如下的条形统计图.根据统计图,回答下列问题: 已知:如图,AD∥BC,∠1+∠2=180°,求证:BC∥EF.
已知:如图,AD∥BC,∠1+∠2=180°,求证:BC∥EF.