题目内容
6.某市需要新建一批公交车候车厅,设计师设计了一种产品(如图1所示),产品示意图的侧面如图2,其中支柱长DC为2.1m,且支柱DC垂直于地面DG,顶棚横梁AE为长1.5m,BC为镶接柱,点B是顶棚的镶接柱与支柱的夹角∠BCD=150°,与顶棚横梁的夹角∠ABC=135°,要求使得横梁一端点E在支柱DC的延长线上,此时经测量得镶接点B与点E的距离为0.35m($\sqrt{2}$≈1.41,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,精确到0.1m).(1)求EC长度;
(2)求点A到地面的距离.
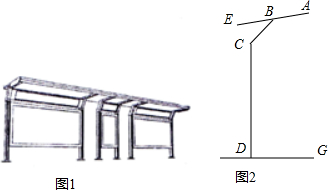
分析 (1)连接EC.可得∠EBC=45°,∠ECB=30°.过点E作EP⊥BC.构建等腰直角三角形,通过解直角三角形得到CE的长度即可;
(2)过点A作AF⊥DG,过点E作EM⊥AF,AM=AE×sin15°.结合图形得到AF=AM+CE+DC.
解答  (1)解:连接EC.可得∠EBC=45°,∠ECB=30°.
(1)解:连接EC.可得∠EBC=45°,∠ECB=30°.
过点E作EP⊥BC.
如图,EP=BE×sin45°≈0.25m.
CE=2EP=0.5m;
(2)解:过点A作AF⊥DG,过点E作EM⊥AF,AM=AE×sin15°.
AF=AM+CE+DC=AE×sin15°+2BE×sin45°+2.1
=0.48+0.50+2.1
=3.0m,
所以点A到地面的距离是3.0m.
点评 本题考查了直角三角形的应用,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
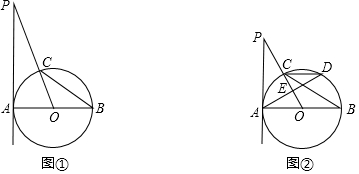
17. 如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
 如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )| A. | ∠3=58° | B. | ∠4=122° | C. | ∠5=52° | D. | ∠2=58° |

 小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)