题目内容
甲，乙，丙三人做某项工作，甲单独做所需时间为乙，丙合做所需时间的3倍，乙独做所需时间甲，丙合做所需2倍，则丙单独做所需时间为甲，乙合做所需时间的（ ）
| A、1.4倍 | B、1.5倍 |
| C、2.5倍 | D、1.8倍 |
考点：三元一次方程组的应用
专题：
分析：等量关系为：甲工作效率×3=乙丙工作效率之和；乙工作效率×2=甲丙工作效率之和，把相关数值代入所得三元一次方程组，用其中一个未知数表示出另两个未知数，进而让工作总量1除以丙的工作效率得到丙单独完成的时间，让工作总量1除以甲乙两人合作做这件工作的工效求得甲乙合作的时间，相除即可．
解答：解：设甲、乙、丙的工作效率分别是x，y，z，则
把z当作已知数，解这个二元一次方程组得 x=
z；y=
z；
∴x+y=
z，
∴丙单独做这件工作的时间是乙甲合作这件工作的
÷
=
=1.4．
故丙单独做做所需时间是甲，乙合作这件工作的1.4倍．
故选A．
|
把z当作已知数，解这个二元一次方程组得 x=
| 3 |
| 5 |
| 4 |
| 5 |
∴x+y=
| 7 |
| 5 |
∴丙单独做这件工作的时间是乙甲合作这件工作的
| 1 |
| z |
| 1 |
| x+y |
| ||
| z |
故丙单独做做所需时间是甲，乙合作这件工作的1.4倍．
故选A．
点评：考查三元一次方程组的应用；根据工作效率得到2个等量关系是解决本题的关键；用一个未知数表示出其余两个未知数是解决本题的突破点；用到的知识点为：工作时间=工作总量÷工作效率．
练习册系列答案
相关题目
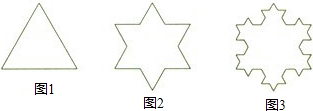
我们来探究“雪花曲线”的有关问题：如图1是长为1的正三角形，现将它作如下变换：取三角形各边的三等分点向形外作没有底边的等边三角形，这样得到一个六角星（如图2）；继续对六角星各边施行相同的变换，得到“雪花形”（如图3）．如此继续下去，第4次变换后得到的图形的周长应等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设S=
+
+…+
+
，则与S最接近的整数是（ ）
1+
|
1+
|
1+
|
1+
|
| A、2005 | B、2006 |
| C、2007 | D、2008 |
设
=
，则(
+
) ÷
=（ ）
| b |
| a+b |
| a-b |
| 3a-b |
| 2a2+b2 |
| 2a2-b2 |
| a2-8b2 |
| a2+8b2 |
| 2a |
| 3b |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
已知|x|=3x+1，则（64x2+48x+9）2005=（ ）
| A、0 | B、1 | C、-1 | D、无法计算 |
如图，奥运五环标志里，包含了圆与圆位置关系中的（ ）| A、相切，内含 |
| B、外切，内含 |
| C、外离，相交 |
| D、相切，相交 |
如果a是方程x2+bx+a=0的根，a≠0，则a+b等于（ ）
A、-
| ||
| B、-1 | ||
C、
| ||
| D、1 |