题目内容
14．已知方程x2-2（n2-1）x-3n=0的两根互为相反数，则n的值为（ ）| A． | n=1 | B． | n=-1 | C． | n=±1 | D． | n=0 |
分析 由题意“两实数根互为相反数”，得方程的两根之和为0．利用根与系数的关系列方程，解方程即可求出m的结果．
解答 解：设方程x2-2（n2-1）x-3n=0的两根为p，q，
由题意可知：p+q=0，
则p+q=-2（n2-1）=0，
解得：n=±1．
故选C．
点评 此题考查了一元二次方程根与系数的关系，设一元二次方程ax2+bx+c=0的两个根为x1，x2，当b2-4ac≥0时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$，熟练掌握根与系数的关系是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．某文具店销售每台进价分别为80元、68元的A，B两种型号的计算器，如表是近两周的销售情况：
（进价、售价均保持不变，利润=销售收入-进货成本）
（1）求A、B两种型号的计算器的销售单价；
（2）若文具店准备用不多于2200元的金额再采购这两种型号的计算器共30台，求A种型号的计算器最多能采购多少台？
（3）在（2）的条件下，文具店销售完这30台计算器能否实现利润为600元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
| 销售时段 | 销售数量 | 销售收入 | |
| 第一周 | 3台A种型号 | 5台B种型号 | 720元 |
| 第二周 | 4台A种型号 | 10台B种型号 | 1240元 |
（1）求A、B两种型号的计算器的销售单价；
（2）若文具店准备用不多于2200元的金额再采购这两种型号的计算器共30台，求A种型号的计算器最多能采购多少台？
（3）在（2）的条件下，文具店销售完这30台计算器能否实现利润为600元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
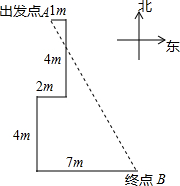如图，小明从点A出发，先向东走1m，然后向南走4m，再向西走2m，最后向东走7m，达到点B，求出发点A到终点B的距离．