题目内容
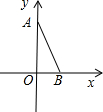 如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )| A、1 | B、2 | C、3 | D、4 |
考点:相似三角形的判定,坐标与图形性质
专题:
分析:根据题意画出图形,根据相似三角形的判定定理即可得出结论.
解答:解:如图①,∠OAB=∠BAC1,∠AOB=∠ABC1时,△AOB∽△ABC1.

如图②,AO∥BC,BA⊥AC2,则∠ABC2=∠OAB,故△AOB∽△BAC2;

如图③,AC3∥OB,∠ABC3=90°,则∠ABO=∠CAB,故△AOB∽△C3BA;

如图④,∠AOB=∠BAC4=90°,∠ABO=∠ABC4,则△AOB∽△C4AB.

故选D.

如图②,AO∥BC,BA⊥AC2,则∠ABC2=∠OAB,故△AOB∽△BAC2;

如图③,AC3∥OB,∠ABC3=90°,则∠ABO=∠CAB,故△AOB∽△C3BA;

如图④,∠AOB=∠BAC4=90°,∠ABO=∠ABC4,则△AOB∽△C4AB.

故选D.
点评:本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
一件工作,甲、乙两人合作需a小时完成,甲单独做需b小时完成,则乙单独做完工作需要的小时数是( )
| A、b-a | ||||
B、
| ||||
C、
| ||||
D、
|
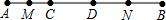 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )| A、7.6cm | B、7.8cm |
| C、8cm | D、8.2cm |
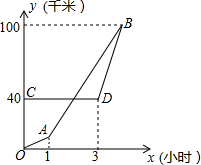 周末,甲从家出发前往与家相距100千米的旅游景点旅游,以10千米/时的速度步行1小时后,改骑自行车以30千米/时的速度继续向目的地出发,乙在甲前面40千米处,在甲出发3小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离y(千米)与甲出发的时间x(小时)之间的函数关系如图所示.
周末,甲从家出发前往与家相距100千米的旅游景点旅游,以10千米/时的速度步行1小时后,改骑自行车以30千米/时的速度继续向目的地出发,乙在甲前面40千米处,在甲出发3小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离y(千米)与甲出发的时间x(小时)之间的函数关系如图所示. 如图所示,线段AB=8cm,C为线段AB上一点,又知M是线段BC的中点,N是线段AC的中点,求MN的长.
如图所示,线段AB=8cm,C为线段AB上一点,又知M是线段BC的中点,N是线段AC的中点,求MN的长. 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,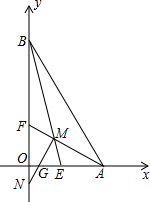 如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.
如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.