题目内容
5.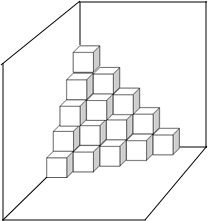 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.(1)第五层有15个小正方体;
(2)从第三层至第六层(含第三层和第六层)共有52个小正方体;
(3)第n层有$\frac{n(n+1)}{2}$个小正方体;
(4)若每个小正方体边长为1分米,共摆放了8层,现要靠墙及地面的部分涂上防锈漆,则防锈漆的总面积为108分米2.
分析 (1)第1个图有1层,共1个小正方体,第2个图有2层,第2层正方体的个数为1+2,第3层正方体的个数为1+2+3,以此类推第五层即可;
(2)第3至6层求出每层个数相加即可;
(3)根据相应规律可得第n层正方体的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$;
(4)共摆放8层,根据靠墙小正方形的面的个数和与地面接触小正方形的面的个数,求出总面数再乘每一个小正方形的面积即可.
解答 解:(1)第1层,共1个小正方体,
第2层正方体的个数为1+2=3,
第3层正方体的个数为:1+2+3=6,
第4层正方体的个数为:1+2+3+4=10,
第5层正方体的个数为:1+2+3+4+5=15,
故答案为:15.
(2)第3正方体的个数为:6,
第4层正方体的个数为:10,
第5层正方体的个数为:15,
第6层正方体的个数为:21,
所以从第三层至第六层(含第三层和第六层)共有:6+10+15+21=52.
故答案为:52.
(3)根据(1)相应规律,可得第n层正方体的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$;
(4)共摆放8层,则靠墙小正方形的面的个数:2×(1+2+3+4+5+6+7+8)=72,
地面接触小正方形的面的个数:1+2+3+4+5+6+7+8=36,
所以靠墙及地面的部分涂上防锈漆的面积为:(72+36)×1=108分米2.
故答案为:108分米2.
点评 此题考查图形规律性的变化,得到第n层正方体的个数的规律是解决本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
10.下列抛物线中,对称轴是x=$\frac{1}{2}$的是( )
| A. | $y=\frac{1}{2}{x^2}$ | B. | y=x2+2x | C. | y=x2+x+2 | D. | y=x2-x-2 |
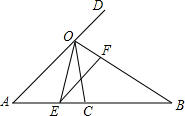 如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E.
如图,∠AOB的平分线OC与线段AB交于点C,点D在AO的延长线上,作射线OE使得OB平分∠DOE,OE交AB于点E. 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.