题目内容
 如图,菱形ABED中,BG⊥DE于G,且GE=
如图,菱形ABED中,BG⊥DE于G,且GE=| 1 |
| 2 |
(1)求证:△ABE是等边三角形;
(2)求证:HE+EF=AE.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)连接BD交AE于点O,利用菱形的性质和已知条件可证明∠DBE=30°,所以∠ABE=60°,所以△ABE为等边三角形;
(2)首先证明△AHE≌△AFB,由全等三角形的性质可得:HE=FB,进而可证明HE+EF=BF+EF=BE=AE.
(2)首先证明△AHE≌△AFB,由全等三角形的性质可得:HE=FB,进而可证明HE+EF=BF+EF=BE=AE.
解答:证明:(1) 连接BD交AE于点O,
连接BD交AE于点O,
∵四边形ABCD是菱形,
∴AB=BE,∠BOE=90°,OE=
AE,
∵GE=
AE,∴OE=GE,
∵BE平分∠DBG,∠BDE=∠DBE,∠BDE=∠DBE,
∴∠DBE=30°,
∴∠ABE=60°,
∴△ABE为等边三角形;
(2)∵∠AEH=∠AFH=∠ABF=60°,
∴A,H,E,F四点共圆,
∴∠HAE=∠HFE,
∵∠HFE+∠AFB=120°,∠AFB+∠FAB=120°,
∴∠HFE=∠FAB,
∴∠HAE=∠FAB,
在△AHE和△AFB中
,
∴△AHE≌△AFB,
∴HE=FB,
∴HE+EF=BF+EF=BE=AE,
 连接BD交AE于点O,
连接BD交AE于点O,∵四边形ABCD是菱形,
∴AB=BE,∠BOE=90°,OE=
| 1 |
| 2 |
∵GE=
| 1 |
| 2 |
∵BE平分∠DBG,∠BDE=∠DBE,∠BDE=∠DBE,
∴∠DBE=30°,
∴∠ABE=60°,
∴△ABE为等边三角形;
(2)∵∠AEH=∠AFH=∠ABF=60°,
∴A,H,E,F四点共圆,
∴∠HAE=∠HFE,
∵∠HFE+∠AFB=120°,∠AFB+∠FAB=120°,
∴∠HFE=∠FAB,
∴∠HAE=∠FAB,
在△AHE和△AFB中
|
∴△AHE≌△AFB,
∴HE=FB,
∴HE+EF=BF+EF=BE=AE,
点评:本题考查了菱形的性质、等边三角形的判定和性质以及全等三角形的判定和性质,题目的综合性较强,题目的难度也不小,对学生的解题能力要求很高.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
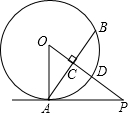 如图:PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4.
如图:PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4. 小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图1),为测量此时风筝的高度,他俩按如下步骤操作:
小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图1),为测量此时风筝的高度,他俩按如下步骤操作:
 一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2=
一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2= 四名选手参加射击预选赛,他们成绩的平均环数
四名选手参加射击预选赛,他们成绩的平均环数