题目内容
△ABC是⊙O的内接三角形;
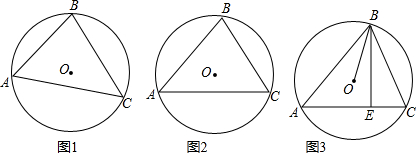
(1)如图1,若BC=4
,AC=7,∠ACB=45°,求⊙O的半径.
(2)如图2,若AB=7,BC=5,AC=8,求∠C的度数及⊙O的半径.
(3)如图3,△ABC是⊙O的内接三角形,BE是AC边上的高,连结BO.
①请证明:∠CBE=∠ABO;
②若AB=7,BC=6,AC=8,请求出⊙O的半径.
(1)如图1,若BC=4
| 2 |
(2)如图2,若AB=7,BC=5,AC=8,求∠C的度数及⊙O的半径.
(3)如图3,△ABC是⊙O的内接三角形,BE是AC边上的高,连结BO.
①请证明:∠CBE=∠ABO;
②若AB=7,BC=6,AC=8,请求出⊙O的半径.

考点:垂径定理,含30度角的直角三角形,勾股定理,圆周角定理
专题:计算题
分析:(1)作直径BD,BH⊥AC于H,连结AD,如图1,在Rt△BCH中,利用等腰直角三角形的性质得CH=BH=
BC=4,则AH=AC-CH=3,接着在Rt△ABH中利用勾股定理计算出AB=5,然后根据圆周角定理,由BD为直径得到∠BAD=90°,∠D=∠ACB=45°,则可判断△ABD为等腰直角三角形,所BD=
AB=5
,即可得到⊙O的半径为
;
(2)作直径BD,BH⊥AC于H,连结AD,如图2,设CH=a,BH=b,则AH=AC-CH=8-a,利用勾股定理得到a2+b2=52①,(8-a)2+b2=72②,利用①-②可解得a=
,在Rt△BCH中,利用含30度的直角三角形三边的关系得到∠CBH=30°,则∠C=60°,再根据圆周角定理得到∠BAD=90°,∠D=∠ACB=60°,利用含30度的直角三角形三边的关系得AD=
AB=
,BD=2AD=
,即可得到⊙O的半径为
;
(3)①证明:作直径BD,连结AD,如图3,先利用垂直定义,由BE⊥AC得到∠CBE+∠C=90°,而∠BAD=90°,∠D=∠ACB,易得∠CBE=∠ABO;
②设CE=a,BE=b,则AE=AC-CE=8-a,利用勾股定理得a2+b2=62①,(8-a)2+b2=72②,利用①-②可解得a=
,接着在Rt△BCE中,利用勾股定理计算出BE=
,然后证明Rt△ABD∽Rt△EBC,利用相似比可计算出AD,从而得到⊙O的半径.
| ||
| 2 |
| 2 |
| 2 |
5
| ||
| 2 |
(2)作直径BD,BH⊥AC于H,连结AD,如图2,设CH=a,BH=b,则AH=AC-CH=8-a,利用勾股定理得到a2+b2=52①,(8-a)2+b2=72②,利用①-②可解得a=
| 5 |
| 2 |
| ||
| 3 |
7
| ||
| 3 |
14
| ||
| 3 |
7
| ||
| 3 |
(3)①证明:作直径BD,连结AD,如图3,先利用垂直定义,由BE⊥AC得到∠CBE+∠C=90°,而∠BAD=90°,∠D=∠ACB,易得∠CBE=∠ABO;
②设CE=a,BE=b,则AE=AC-CE=8-a,利用勾股定理得a2+b2=62①,(8-a)2+b2=72②,利用①-②可解得a=
| 51 |
| 16 |
21
| ||
| 16 |
解答:解:(1) 作直径BD,BH⊥AC于H,连结AD,如图1,
作直径BD,BH⊥AC于H,连结AD,如图1,
在Rt△BCH中,CH=BH=
BC=
•4
=4,
∴AH=AC-CH=7-4=3,
在Rt△ABH中,AB=
=5,
∵BD为直径,
∴∠BAD=90°,
∵∠D=∠ACB=45°,
∴△ABD为等腰直角三角形,
∴BD=
AB=5
,
∴⊙O的半径为
;
(2)作直径BD,BH⊥AC于H,连结AD,如图2,
设CH=a,BH=b,则AH=AC-CH=8-a,
在Rt△BCH中,a2+b2=52①,
在Rt△BAH中,(8-a)2+b2=72②,
①-②得-64+16a=-24,解得a=
,
在Rt△BCH中,∵BC=5,CH=
,
∴∠CBH=30°,
∴∠C=60°,
∵BD为直径,
∴∠BAD=90°,
∵∠D=∠ACB=60°,
∴AD=
AB=
,
∴BD=2AD=
∴⊙O的半径为
;
(3)①证明:作直径BD,连结AD,如图3,
∵BE⊥AC,
∴∠CBE+∠C=90°,
∵BD为直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵∠D=∠ACB,
∴∠CBE=∠ABO;
②设CE=a,BE=b,则AE=AC-CE=8-a,
在Rt△BCE中,a2+b2=62①,
在Rt△BAE中,(8-a)2+b2=72②,
①-②得-64+16a=-13,解得a=
,
在Rt△BCE中,∵BC=6,CE=
,
∴BE=
=
,
∵∠CBE=∠ABD,
∴Rt△ABD∽Rt△EBC,
∴
=
,
∴AD=
=
,
∴⊙O的半径为
.
 作直径BD,BH⊥AC于H,连结AD,如图1,
作直径BD,BH⊥AC于H,连结AD,如图1,在Rt△BCH中,CH=BH=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴AH=AC-CH=7-4=3,
在Rt△ABH中,AB=
| AH2+BH2 |
∵BD为直径,
∴∠BAD=90°,
∵∠D=∠ACB=45°,
∴△ABD为等腰直角三角形,
∴BD=
| 2 |
| 2 |
∴⊙O的半径为
5
| ||
| 2 |
(2)作直径BD,BH⊥AC于H,连结AD,如图2,

设CH=a,BH=b,则AH=AC-CH=8-a,
在Rt△BCH中,a2+b2=52①,
在Rt△BAH中,(8-a)2+b2=72②,
①-②得-64+16a=-24,解得a=
| 5 |
| 2 |
在Rt△BCH中,∵BC=5,CH=
| 5 |
| 2 |
∴∠CBH=30°,
∴∠C=60°,
∵BD为直径,
∴∠BAD=90°,
∵∠D=∠ACB=60°,
∴AD=
| ||
| 3 |
7
| ||
| 3 |
∴BD=2AD=
14
| ||
| 3 |
∴⊙O的半径为
7
| ||
| 3 |
(3)①证明:作直径BD,连结AD,如图3,
∵BE⊥AC,
∴∠CBE+∠C=90°,
∵BD为直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵∠D=∠ACB,
∴∠CBE=∠ABO;
②设CE=a,BE=b,则AE=AC-CE=8-a,
在Rt△BCE中,a2+b2=62①,
在Rt△BAE中,(8-a)2+b2=72②,

①-②得-64+16a=-13,解得a=
| 51 |
| 16 |
在Rt△BCE中,∵BC=6,CE=
| 51 |
| 16 |
∴BE=
| BC2-CE2 |
21
| ||
| 16 |
∵∠CBE=∠ABD,
∴Rt△ABD∽Rt△EBC,
∴
| AD |
| BC |
| AB |
| AE |
∴AD=
| 6×7 | ||||
|
32
| ||
| 15 |
∴⊙O的半径为
16
| ||
| 15 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
下面说法正确的有( )
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
| A、4个 | B、3个 | C、2个 | D、1个 |
若x<y成立,则下列不等式成立的是( )
| A、-3x<-3y |
| B、x-2<y-2 |
| C、-(x-2)<-(y-2) |
| D、-x+2<-y+2 |
 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC与BD相交于点E,AC=BC,DE=3,AD=5,则⊙O的半径为
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC与BD相交于点E,AC=BC,DE=3,AD=5,则⊙O的半径为 如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.
如图是一个几何体的三视图,其中主视图、左视图都是腰为13cm,底为10cm的等腰三角形,求这个几何体的体积.