题目内容
 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC与BD相交于点E,AC=BC,DE=3,AD=5,则⊙O的半径为
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AC与BD相交于点E,AC=BC,DE=3,AD=5,则⊙O的半径为考点:相似三角形的判定与性质,全等三角形的判定与性质,圆周角定理
专题:
分析:如图,作辅助线;证明CF⊥AB(垂径定理的推论);证明AD⊥AB,得到AD∥OC,△ADE∽△COE;得到AD:CO=DE:OE,求出CO的长,即可解决问题.
解答: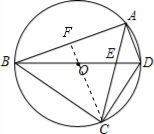 解:如图,连接CO并延长,交AB于点F;
解:如图,连接CO并延长,交AB于点F;
∵AC=BC,
∴CF⊥AB(垂径定理的推论);
∵BD是⊙O的直径,
∴AD⊥AB;设⊙O的半径为λ;
∴AD∥OC,△ADE∽△COE,
∴AD:CO=DE:OE,
而DE=3,AD=5,OE=λ-3,CO=λ,
∴5:λ=3:(λ-3),
解得:λ=
,
故答案为
.
 解:如图,连接CO并延长,交AB于点F;
解:如图,连接CO并延长,交AB于点F;∵AC=BC,
∴CF⊥AB(垂径定理的推论);
∵BD是⊙O的直径,
∴AD⊥AB;设⊙O的半径为λ;
∴AD∥OC,△ADE∽△COE,
∴AD:CO=DE:OE,
而DE=3,AD=5,OE=λ-3,CO=λ,
∴5:λ=3:(λ-3),
解得:λ=
| 15 |
| 2 |
故答案为
| 15 |
| 2 |
点评:该题主要考查了相似三角形的判定及其性质、垂径定理的推论等几何知识点的应用问题;解题的关键是作辅助线,构造相似三角形,灵活运用有关定来分析、判断.

练习册系列答案
相关题目
 如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )
如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )| A、|b|>|a| |
| B、a-b>0 |
| C、ab>0 |
| D、a+b<0 |
下列图形中不可能是几何体的是( )
| A、三棱柱 | B、圆柱 | C、正方形 | D、球 |

 如图,EF、AC、BD交于一点G,AD∥BC∥EF,
如图,EF、AC、BD交于一点G,AD∥BC∥EF, 如图,已知正方形ABCD,以CD为边作等边△DEC,并连接AE、BC,求S△EMN:S△ADN.
如图,已知正方形ABCD,以CD为边作等边△DEC,并连接AE、BC,求S△EMN:S△ADN.