题目内容
1.将长为10米的梯子斜靠在墙上,若梯子的上端到墙的底端的距离为8米,则梯子的底端到墙的底端的距离为6m.NN#分析 在Rt△ABC中,利用勾股定理即可求出BC的值.
解答 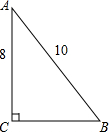 解:在Rt△ABC中,AB2=AC2+BC2,
解:在Rt△ABC中,AB2=AC2+BC2,
∵AB=10m,AC=8m,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6(m),
即梯子的底端到墙的底端的距离为6m.
故答案为:6m.
点评 本题考查了勾股定理的应用,解答本题的关键是掌握勾股定理在直角三角形中的表达式.

练习册系列答案
相关题目
12.日历中同一竖列相邻三个数的和不可能是( )
| A. | 72 | B. | 26 | C. | 24 | D. | 45 |
13.若方程(m-1)${x^{{m^2}+1}}$-x+3=0是关于x的一元二次方程,那么m的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 以上都不对 |
11.计算:(a2b)3的结果是( )
| A. | a6b | B. | a6b3 | C. | a5b3 | D. | a2b3 |
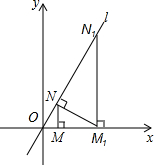 如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).
如图,已知直线l:y=$\sqrt{3}$x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;则 M1的坐标为(8,0).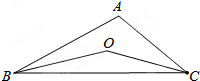 如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.
如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.