题目内容
11.已知|x-2|+(y+4)2+$\sqrt{x+y-2z}$=0,求(xz)y的平方根.分析 根据非负数的性质列式求出x、y、z,然后代入代数式求出代数式的值,再根据平方根的定义解答.
解答 解:由题意得,x-2=0,y+4=0,x+y-2z=0,
解得x=2,y=-4,z=-1,
所以(xz)y=(-2)-4=$\frac{1}{16}$,
所以(xz)y的平方根是±$\sqrt{\frac{1}{16}}$=±$\frac{1}{4}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
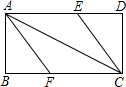 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连结AF和CE. 如图,四边形ABCD中,∠B=∠D=90°,∠C=60°,AB=11,AD=2,求BC的长.
如图,四边形ABCD中,∠B=∠D=90°,∠C=60°,AB=11,AD=2,求BC的长. 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,AC=BE.求证:CD+AE=BD.
如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,AC=BE.求证:CD+AE=BD.