题目内容
6．甲乙二人在环形跑道上同时同地出发，同向跑步，甲的速度为7米/秒，乙的速度为6.5米/秒，若跑道一周的长为400米，设经过x秒后甲乙两人第一次相遇，则列方程为7x-6.5x=400．分析 在环形跑道上两人同向而行相遇属于追及问题，等量关系为：甲路程-乙路程=400，依此列出方程即可．
解答 解：设经过x秒后甲乙两人第一次相遇，则：
7x-6.5x=400．
故答案为7x-6.5x=400．
点评 本题考查了由实际问题抽象出一元一次方程，解题的关键是弄清题意找到等量关系．
练习册系列答案
相关题目
16．下列说法不正确的是（ ）
| A． | 3是9的平方根 | B． | 无理数都是无限小数 | ||
| C． | （3-π）2的算术平方根是3-π | D． | 实数与数轴上的点是一一对应的 |
14．下列等式从左到右的变形中，属于因式分解的是（ ）
| A． | （x+1）（x-1）=x2-1 | B． | x2+2x+1=（x+1）2 | C． | x2+2x-1=x（x+2）-1 | D． | x （x-1）=x2-x |
如图，在正方形网格图中，若⊙O的半径为2，则阴影部分两个小扇形的面积之和为π．（结果保留π）
15．
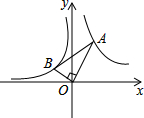如图，已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上，第二象限的点B在反比例函数y=$\frac{k}{x}$上，且OA⊥OB，$\frac{OB}{OA}$=$\frac{3}{4}$，则k的值为（ ）
如图，已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上，第二象限的点B在反比例函数y=$\frac{k}{x}$上，且OA⊥OB，$\frac{OB}{OA}$=$\frac{3}{4}$，则k的值为（ ）| A． | $\frac{9}{4}$ | B． | -$\frac{9}{4}$ | C． | -$\frac{3}{4}$ | D． | -3 |
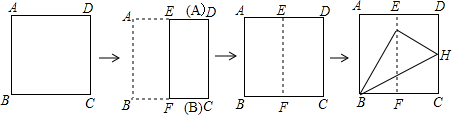
16．如图，先将一张长方形的纸沿虚线对折，再对折，然后按图中虚线剪下，将剪下的纸展开，一定可以得到一个（ ）
| A． | 菱形 | B． | 矩形 | C． | 正方形 | D． | 梯形 |