题目内容
5.若y=ax2+bx+c是关于x的二次函数且a为整数,并且不等式4x≤ax2+bx+c≤2(x2+1)在实数范围内恒成立,则二次函数的解析式为( )| A. | y=x2+2x+1 | B. | y=x2+2x+2 | C. | y=2x2+2x+1 | D. | y=2x2+2x+2 |
分析 由ax2+(b-4)x+c≥0在实数范围内恒成立,可知a>0,且(b-4)2-4ac≤0,由(2-a)x2-bx-c+2≥0在实数范围内恒成立,可知2-a>0,且b2-4(2-a)(c-2)≤0,故此可得到a=1,从而可排除C、D,然后将b=2,c=1和b=2,c=2代入(b-4)2-4ac≤0和b2-4(2-a)(c-2)≤0验证即可判断.
解答 解:由4x≤ax2+bx+c得:ax2+(b-4)x+c≥0,
∵不等式在实数范围内恒成立,
∴a>0,且(b-4)2-4ac≤0.
∵ax2+bx+c≤2(x2+1),
∴(2-a)x2-bx-c+2≥0.
∵不等式在实数范围内恒成立,
∴2-a>0,且b2-4(2-a)(c-2)≤0.
又∵a为整数,
∴a=1.
故可排除C、D.
∴(b-4)2-4c≤0且b2-4(c-2)≤0.
将b=2,c=1代入不等式成立,故A正确.
将b=2,c=2代入不等式时b2-4(c-2)≤0不成立,故D错误.
故选:A.
点评 本题主要考查的是二次函数和不等式的关系,将不等式问题转化为二次函数与x轴有无交点问题是解题的关键.

练习册系列答案
相关题目
16.正多边形的一个外角等于30°,则这个多边形的内角和为( )
| A. | 1080 | B. | 1440 | C. | 1620 | D. | 1800 |
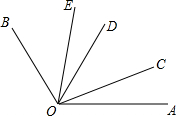 如图,OC,OD,OE是∠AOB内部的三条射线,下面关于∠EOC的表述:①∠EOC=∠BOC-∠BOE;②∠EOC=∠EOD+∠COD;③∠EOC=∠BOC+∠AOE-∠AOB;④∠EOC=∠AOB-∠BOD,其中表述正确的个数有( )
如图,OC,OD,OE是∠AOB内部的三条射线,下面关于∠EOC的表述:①∠EOC=∠BOC-∠BOE;②∠EOC=∠EOD+∠COD;③∠EOC=∠BOC+∠AOE-∠AOB;④∠EOC=∠AOB-∠BOD,其中表述正确的个数有( ) 已知二次函数y=$\frac{1}{2}$x2+3x+2的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求四边形ACBD的面积.
已知二次函数y=$\frac{1}{2}$x2+3x+2的图象与x轴交于A、B两点,与y轴交于D点,顶点为C,求四边形ACBD的面积.