题目内容
13.计算(1)$\sqrt{3}$×($\sqrt{6}$+$\sqrt{3}$)-$\sqrt{2}$
(2)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(3)($\sqrt{3}$-1)2+($\sqrt{3}$+2)2-(2$\sqrt{3}$-1)($\sqrt{3}$+2)
(4)3($\sqrt{5}$-π)0-$\frac{\sqrt{20}-\sqrt{15}}{5}$+(-1)2015.
分析 (1)先算乘法,再进一步化简合并;
(2)先算乘除,再算加减即可;
(3)利用完全平方公式和二次根式的乘法计算,再进一步合并即可;
(4)先算0指数幂、乘方、化简二次根式,再进一步计算加减合并即可.
解答 解:(1)原式=3$\sqrt{2}$+3+$\sqrt{2}$
=4$\sqrt{2}$+3;
(2)原式=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(3)原式=4-2$\sqrt{3}$+7+4$\sqrt{3}$-(4+3$\sqrt{3}$)
=11+2$\sqrt{3}$-4-3$\sqrt{3}$
=7-$\sqrt{3}$;
(4)原式=3-$\frac{2}{5}$$\sqrt{5}$+$\frac{\sqrt{15}}{5}$-1
=2-$\frac{2}{5}$$\sqrt{5}$+$\frac{\sqrt{15}}{5}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
相关题目
4.顺次连结矩形四边的中点所得的四边形是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 以上都不对 |
1. 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )| A. | 70° | B. | 68° | C. | 60° | D. | 72° |
8.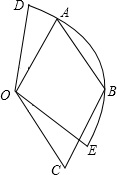 如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
 如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )
如图,四边形OCBC是菱形,点A、B在以点O为圆心的圆弧DE上,若AO=3,∠COE=∠DOA,则扇形ODE的面积为( )| A. | $\frac{2}{3}$π | B. | 2π | C. | $\frac{5}{2}$π | D. | 3π |
18.点P(2,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下列各式中,计算正确的是( )
| A. | a3•a4=a7 | B. | a6÷a3=a2 | C. | (a3)4=a7 | D. | (ab)3=ab3 |
3.在下面四个几何体中,俯视图是三角形的是( )


| A. | ① | B. | ② | C. | ③ | D. | ④ |
 如图,已知∠1=∠2,∠3=80°,则∠4=80°.
如图,已知∠1=∠2,∠3=80°,则∠4=80°.