题目内容
8.下列各组不能构成直角三角形的三边长的是( )| A. | 5,12,13 | B. | 12,13,14 | C. | 3,4,5 | D. | 7,24,25 |
分析 欲判断能否构成直角三角形,只需验证两小边的平方和是否等于最长边的平方.
解答 解:A、52+122=132,能构成直角三角形;
B、122+132≠142,不能构成直角三角形;
C、32+42=52,能构成直角三角形;
D、72+242=252,能构成直角三角形.
故选B.
点评 本题考查了利用勾股定理逆定理判定直角三角形的方法.在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
相关题目
19. 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
 如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )
如图所示,在矩形ABCD中,AB=10,BC=6,点E、F在DC边上,连接AF、BE交于点P,若EF=$\frac{1}{2}$DC,则图中阴影部分的面积为( )| A. | 50 | B. | 45 | C. | 40 | D. | 35 |
16. 如图,直线AB,CD交于O,EO⊥AB于O,若∠1=73°,则∠2等于( )
如图,直线AB,CD交于O,EO⊥AB于O,若∠1=73°,则∠2等于( )
 如图,直线AB,CD交于O,EO⊥AB于O,若∠1=73°,则∠2等于( )
如图,直线AB,CD交于O,EO⊥AB于O,若∠1=73°,则∠2等于( )| A. | 27° | B. | 25° | C. | 23° | D. | 17° |
13.由$\frac{x}{3}$-y=6,可以得到用x表示y的式子是( )
| A. | x=18-y | B. | x=18-3y | C. | y=$\frac{x}{3}$-6 | D. | y=$\frac{x}{3}$+6 |
20.下列计算正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{9}$=±3 | C. | $\root{3}{-8}$=-2 | D. | $\sqrt{25}$-$\sqrt{16}$=$\sqrt{9}$ |
17.以下命题中是真命题的是( )
| A. | 内错角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 两个角的和等于平角时,这两个角互为补角 | |
| D. | 两个锐角的和是锐角 |
18. 如图,多边形ABCDEF与AGHEMN都是正六边形,则∠FAN的度数为( )
如图,多边形ABCDEF与AGHEMN都是正六边形,则∠FAN的度数为( )
 如图,多边形ABCDEF与AGHEMN都是正六边形,则∠FAN的度数为( )
如图,多边形ABCDEF与AGHEMN都是正六边形,则∠FAN的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
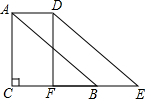 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )