题目内容
16．△ABC中，AB=15，AC=20，BC边上的高AD=12，则△ABC的周长为42或60．分析 已知三角形两边的长和第三边的高，未明确这个三角形为钝角还是锐角三角形，所以需分情况讨论，即∠ABC是钝角还是锐角，然后利用勾股定理求解．
解答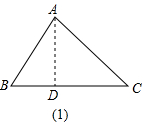 
解：如图（1），△ABC中，AB=15，AC=20，BC边上高AD=12，
在Rt△ABD中AB=15，AD=12，
由勾股定理得，BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=9，
在Rt△ADC中AC=20，AD=12，
由勾股定理得，DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=16，
则BC的长为BD+DC=9+16=25，
△ABC的周长为：15+20+25=60，
如图（2），同（1）的作法相同，BC=7，
△ABC的周长为：15+20+7=42，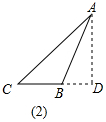
故答案为：42或60．
点评 本题主要考查了勾股定理，解决问题的关键是在直角三角形中用勾股定理求得线段的长．当已知条件中没有明确角的大小时，要注意讨论．
练习册系列答案
相关题目
6．下列计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B． | 2+$\sqrt{2}$=2$\sqrt{2}$ | C． | 3$\sqrt{2}$-$\sqrt{2}$=3 | D． | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
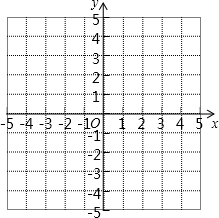已知等边△ABC两个顶点的坐标为A（-4，0），B（0，0），且点C在第二象限．求：
如图，六边形ABCDEF中，AB∥DE，BC∥EF，CD∥AF．现有以下结论：①∠A+∠C+∠E=360°；②∠B+∠C+∠D=360°；③AB=DE．其中正确的结论有（ ）
如图1，三条直线两两相交，且不共点，则图中同旁内角有6对；如图2，四条直线两两相交，任三条直线不经过同一点，则图中的同旁内角有24对．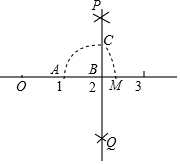
如图，数轴上点A、B对应的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径作圆弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，当点M在点B的右侧时，点M对应的数是$\sqrt{5}$．