题目内容
10.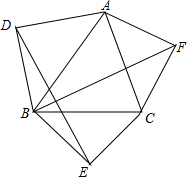 如图,以△ABC三边为底向外作等腰直角三角形,连接DE、BF.
如图,以△ABC三边为底向外作等腰直角三角形,连接DE、BF.求证:DE=BF,DE⊥BF.
分析 先构造正方形ADBP,连接DP,EP,通过判定△PBE∽△ABC,得出∠BPE=∠BAC,∠BEP=∠BCA,$\frac{PE}{AC}$=$\frac{\sqrt{2}}{2}$,进而根据SAS判定△ABF≌△PDE,即可得出BF=DE,∠ABF=∠PDE,再根据DP⊥AB,且AB、DE交于一点,可得DE⊥BF.
解答 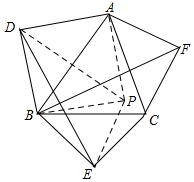 解:将△ABD沿着AB翻折,得正方形ADBP,连接DP,EP,则DP=BA,DP⊥BA,
解:将△ABD沿着AB翻折,得正方形ADBP,连接DP,EP,则DP=BA,DP⊥BA,
∵∠ABP=∠CBE=45°,
∴∠PBE=∠ABC,
又∵$\frac{BP}{BA}$=$\frac{BE}{BC}$=$\frac{\sqrt{2}}{2}$,
∴△PBE∽△ABC,
∴∠BPE=∠BAC,∠BEP=∠BCA,$\frac{PE}{AC}$=$\frac{\sqrt{2}}{2}$,
∴PE=$\frac{\sqrt{2}}{2}$AC,
又∵AF=$\frac{\sqrt{2}}{2}$AC,
∴PE=AF,
∵∠DPE=∠DPB+∠BPE=45°+∠BPE,∠BAF=∠CAF+∠BAC=45°+∠BAC,
∴∠DPE=∠BAF,
在△ABF和△PDE中,
$\left\{\begin{array}{l}{AB=PD}\\{∠BAF=∠DPE}\\{AF=PE}\end{array}\right.$,
∴△ABF≌△PDE(SAS),
∴BF=DE,∠ABF=∠PDE,
又∵DP⊥AB,且AB、DE交于一点,
∴DE⊥BF.
点评 本题主要考查了等腰直角三角形,全等三角形的判定与性质,相似三角形的判定与性质以及三角形内角和定理的综合应用,解决问题的关键是作辅助线构造正方形以及全等三角形、相似三角形,依据全等三角形的对应边相等,对应角相等进行求解.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
2.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.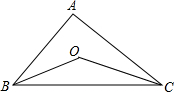 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )| A. | 140° | B. | 120° | C. | 90° | D. | 80° |
 如图,它是一个数值转换机,若输入的a值为$\sqrt{2}$,则输出的结果应为-$\frac{2\sqrt{3}}{3}$.
如图,它是一个数值转换机,若输入的a值为$\sqrt{2}$,则输出的结果应为-$\frac{2\sqrt{3}}{3}$.