题目内容
16.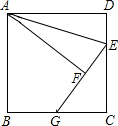 如图,正方形ABCD中,E为CD上一点,以AE为对称轴将△ADE翻折得到△AFE,延长EF交BC于G,若BG=CG,则sin∠EGC=$\frac{4}{5}$.
如图,正方形ABCD中,E为CD上一点,以AE为对称轴将△ADE翻折得到△AFE,延长EF交BC于G,若BG=CG,则sin∠EGC=$\frac{4}{5}$.
分析 利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出Rt△ABG≌Rt△AFG,得出BG=FG,设CG为x,BG=FG=x,由勾股定理得出CE,即可得出结果.
解答 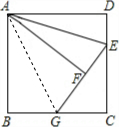 解:连接AG,
解:连接AG,
∵将△ADE翻折得到△AFE,
∴AB=AD=AF,AG=AG,∠D=∠B=∠AFG=90°,
在Rt△ABG与Rt△AFG中,
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
BG=FG,
设CG为x,则GF=BG=x,
在Rt△EGC中,CG2+EC2=EG2,
即x2+CE2=(3x-CE)2,
解得,CE=$\frac{4}{3}$x,
∴EG=$\frac{5}{3}$x,
∴sin∠EGC=$\frac{EC}{EG}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 此题主要考查了正方形的性质、全等三角形的判定与性质、勾股定理;熟练掌握正方形的性质,证明三角形全等和运用勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
8.下列各式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | ||
| C. | -x2+4xy-4xy2=-(x-2y)2 | D. | a2+ab+b2=(a+b)2 |
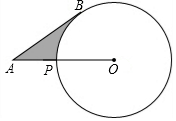 如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2