题目内容
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（ ）
A. k＞﹣1 B. k＞﹣1且k≠0 C. k＜1 D. k＜1且k≠0
B 【解析】试题解析：∵关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根， ∴k≠0且△＞0，即（-2）2-4×k×（-1）＞0， 解得k＞-1且k≠0． ∴k的取值范围为k＞-1且k≠0． 故选B.在a2□4a□4的空格□中，任意填上“+”或“﹣”，在所有得到的代数式中，能构成完全平方式的概率是（ ）
A. 1 B.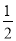 
C. 
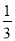D.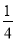 
已知正六边形的边长为2，则它的内切圆的半径为（ ）
A. 1 B.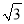 
C. 2 D. 2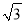
已知一组数据：16，15，16，14，17，16，15，则众数是（ ）
A. 17 B. 16 C. 15 D. 14
查看答案已知⊙O的半径为2，直线l上有一点P满足PO＝2，则直线l与⊙O的位置关系是（ ）
A. 相切 B. 相离 C. 相离或相切 D. 相切或相交
查看答案方程：x（x+1）=3（x+1）的解的情况是（ ）
A．x=﹣1 B．x=3 C．x1=﹣1，x2=3 D．以上答案都不对
查看答案 试题属性- 题型：单选题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
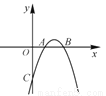
步步高达标卷系列答案如图，对称轴为x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．
（1）求点B的坐标．
（2）已知a=1，C为抛物线与y轴的交点．
①若点P在抛物线上，且S△POC=4S△BOC，求点P的坐标．
②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．
为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+80．设这种产品每天的销售利润为w元．
（1）求w与x之间的函数关系式．
（2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？
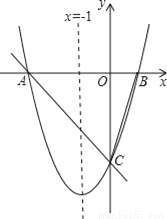
查看答案宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军，让全校师生倍受鼓舞．在一次与第25中学的比赛中，运动员小涛在距篮下4米处跳起投篮，如图所示，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05米．
（1）建立如图所示的直角坐标系，求抛物线的表达式；
（2）运动员小涛的身高是1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，小涛跳离地面的高度是多少？
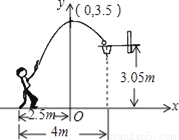
如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？
已知抛物线y=ax2+bx+c与x轴交于点A(1，0)，B(3，0)，且过点C(0，-3).
(1)求抛物线的解析式和顶点坐标；
(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=-x上，并写出平移后抛物线的解析式.
已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
查看答案 试题属性- 题型：解答题
- 难度：困难
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
有四包真空包装的火腿肠，每包以标准质量450g为基准，超过的克数记作正数，不足的克数记作负数．下面的数据是记录结果，其中与标准质量最接近的是（ ）
A. +2 B. ﹣3 C. +4 D. ﹣1
D 【解析】试题解析：因为|+2|=2，|-3|=3，|+4|=4，|-1|=1， 由于|-1|最小，所以从轻重的角度看，质量是-1的工件最接近标准工件． 故选D．如图，是一个正方形盒子的展开图，若要在展开后的其中的三个正方形A、B、C内分别填入适当的数，使得展开图折成正方体后相对的面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为（ ）
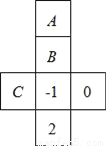
A. 1，﹣2，0 B. 0，﹣2，1 C. ﹣2，0，1 D. ﹣2，1，0
查看答案单项式﹣3πxy2z3的系数和次数分别是（ ）
A. ﹣π，5 B. ﹣1，6 C. ﹣3π，6 D. ﹣3，7
查看答案下列各题运算正确的是（ ）
A. 2a+b=2ab B. 3x2﹣x2=2 C. 7mn﹣7mn=0 D. a+a=a2
查看答案11月2日我市一天的最高气温是12℃，最低气温是﹣1℃，那么这一天的最高气温比最低气温高（ ）
A. ﹣13℃ B. ﹣11℃ C. 13℃ D. 11℃
查看答案长城总长约为6 700 000米，用科学记数法表示正确的是（ ）
A. 6.7×108米 B. 6.7×107米 C. 6.7×106米 D. 6.7×105米
查看答案 试题属性- 题型：单选题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解方程：（1）2x2﹣5x+2=0；
（2）x+3﹣x（x+3）=0．
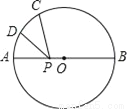
(1)x1=2，x2=;(2)x1=﹣3，x2=1 【解析】试题解析： （1）题选用“公式法”来解（也可用其它方法）； （2）题根据题目特点，选用“因式分解法”来解. 试题解析： （1）∵在方程中， ， ∴， ∴， ∴； （2）原方程可变形为： ， ∴或， 解得： .如图，AB是⊙O的直径，点C是半圆上的一个三等分点，点D是
的中点，点P是直径AB上一点，若⊙O的半径为2，则PC+PD的最小值是_____．
写出一个以﹣1和﹣2为两根的一元二次方程（二次项系数为1）_____．
查看答案某种药品原来售价60元，连续两次降价后售价为48.6元，若每次下降的百分率相同，则这个百分率是_____．
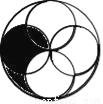
查看答案如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为_____平方厘米．
若m是关于x的一元二次方程ax2+bx﹣5=0的一个根，则代数式am2+bm﹣7的值为_____。
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若圆锥的底面半径为3，母线长为6，则圆锥的侧面积等于_____．
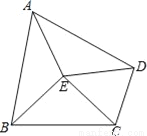
18π 【解析】试题分析：根据圆锥的侧面积就等于经母线长乘底面周长的一半．依此公式计算即可解决问题． 圆锥的侧面积=6×6π÷2=18π． 故答案为：18π．已知四边形ABCD内有一点E，满足EA=EB=EC=ED，且∠BCD=130°，那么∠BAD的度数为_____．
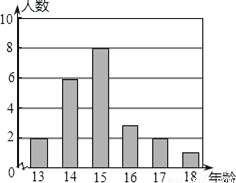
某校男子足球队队员的年龄分布为如图的条形图，则这些队员年龄的众数、中位数分别是_____。
现有60件某种产品，其中有3件次品，那么从中任意抽取1件产品恰好抽到次品的概率是_____。
查看答案如图，水平地面上有一面积为30πcm2的灰色扇形OAB，其中OA=6cm，且OA垂直于地面，将这个扇形向右滚动（无滑动）至点B刚好接触地面为止，则在这个滚动过程中，点O移动的距离是（ ）
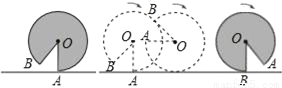
A. 10πcm B. 20πcm C. 24πcm D. 30πcm
查看答案若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（ ）
A. k＞﹣1 B. k＞﹣1且k≠0 C. k＜1 D. k＜1且k≠0
查看答案 试题属性- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
方程：x（x+1）=3（x+1）的解的情况是（ ）
A．x=﹣1 B．x=3 C．x1=﹣1，x2=3 D．以上答案都不对
C 【解析】 试题分析：∵x（x+1）=3（x+1） ∴x（x+1）﹣3（x+1）=0 ∴（x+1）（x﹣3）=0 ∴x1=﹣1，x2=3 故选：C．已知：m，x，y满足：（1）
；（2）﹣2a2by+1与7b3a2是同类项．
求代数式：2x2﹣6y2+m（xy﹣9y2）﹣（3x2﹣3xy+7y2）的值．
查看答案某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在A处，规定向北方向为正，当天行驶情况记录如下（单位：千米）：+10，﹣8，+7，﹣15，+6，﹣16，+4，﹣2
（1）A处在岗亭何方？距离岗亭多远？
（2）若摩托车每行驶1千米耗油0.5升，这一天共耗油多少升？
查看答案化简求值：（2x2y﹣4xy2）﹣（﹣3xy2+x2y），其中x=﹣1，y=2．
查看答案如果规定符号“*”的意义是：a*b=
，试求2*（﹣4）的值．
计算题
（1）﹣8﹣6+22﹣9．
（2）（﹣
+
﹣
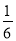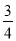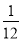）×48．
（3）|﹣0.75|+（﹣3）﹣（﹣0.25）+|﹣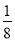
|+
．
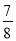（4）﹣22+3×（﹣1）4﹣（﹣4）×5．
（5）（7m2n﹣5mn）﹣（4m2n﹣5mn）
（6）
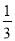（9a﹣3）+2（a+1）．
- 题型：单选题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
数轴上到点﹣3的距离是3个单位长度的点表示的数是_____．
0或﹣6． 【解析】试题分析：在数轴上两点所表示的数的差的绝对值为这两个点之间的距离．设这个点表示的数为x，则，则，解得：x=0或-6，即这个点表示的数为0或-6．已知单项式3amb2与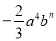
的和是单项式，那么m=_____，n=_____．
某种零件，标明要求是φ20±0.02 mm（φ表示直径，单位：毫米），经检查，一个零件的直径是19.9 mm，该零件________ （填“合格”或“不合格”）．
查看答案我国2006年参加高考报名的总人数约为950万人，则该人数可用科学记数法表示为_____人．
查看答案若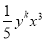
与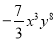
是同类项，则k=_____．
单项式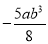
的系数是 ，次数是 ．
- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
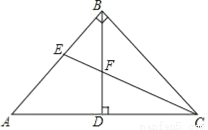
如图，在△ABC中，∠ABC=90°，AB=BC，BD⊥AC于点D；CE平分∠ACB，交AB于点E，交BD于点F．
（1）求证：△BEF是等腰三角形；
（2）求证：BD=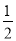
（BC+BF）．
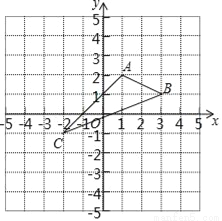
在平面直角坐标系中，A（1，2）、B（3，1）、C（﹣2，﹣1）．
（1）在图中作出△ABC关于y轴对称的△A1B1C1；
（2）写出△ABC关于x轴对称△A2B2C2的各项点坐标A2 ，B2 ，C2 ；
（3）求△ABC的面积．
（1）已知x+y=15，x2+y2=113，求x2﹣3xy+y2的值；
（2）先化简，再求值：（2x﹣1）2﹣（3x+1）（3x﹣1）+5x（x﹣1），x=﹣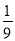
．
（1）（﹣2a2）3+2a2•a4；
（2）（x+y）2﹣（x+y）（x﹣y）
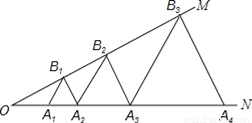
查看答案如图，已知∠MON=30°，点A1、A2、A3，…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形，若OA1=1，则△A2016B2016A2017的边长为_____．
已知a2﹣a﹣1=0，则a2﹣a+2017=_____．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
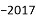
A.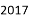 
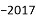
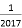D.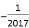 
已知多项式A，B，计算A﹣B．某同学做此题时误将A﹣B看成了A+B，求得其结果为A+B=3m2﹣2m﹣5，若B=2m2﹣3m﹣2，请你帮助他求得正确答案．
查看答案已知|a﹣2|+（b+1）2=0，求5ab2﹣|2a2b﹣（4ab2﹣2a2b）|的值．
查看答案出租车司机老李某天上午营运全是在东西走向的胜利路上进行，如果规定向东为正，向西为负，他这天上午行车里程（单位：公里 ）如下：
+8，+4，﹣10，﹣8，+6，﹣2，﹣5，﹣7，+4，+6，﹣8，﹣9
（1）将第几名乘客送到目的地时，老王刚好回到上午出发点？
（2）将最后一名乘客送 到目的地时，老王距上午出发点多远？
（3）若汽车耗油量为0.4升/公里，这天上午老王耗油多少升？
查看答案先化简，再求值．
（1）
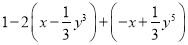，其中x=﹣
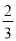，y=﹣1．
（2）﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中a=1，b=﹣2．
查看答案若有理数m、n在数轴上的位置如图所示，请化简：|m+n|+|m﹣n|﹣|n|．
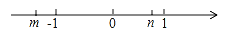
- 题型：单选题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧