题目内容
14．
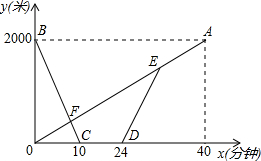甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路L步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图．（1）求小亮从乙地到甲地过程中y（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式．
分析 （1）设一次函数的解析式为y=kx+b，利用待定系数法解答即可；
（2）求出小亮和小明的速度后，得出两人间距与时间之间的关系式，化简解出解析式即可．
解答 解：设小亮与甲地的距离为y（米）与x（分钟）之间的函数关系式为y=kx+b，
则代入点（0，2000）和（10，0）得
$\left\{\begin{array}{l}{b=2000}\\{k=-200}\end{array}\right.$，
所以y=-200x+2000；（0≤x≤10）
（2）由图象可得小亮的速度为：2000÷10=200米/分钟；小明的速度为：2000÷40=50米/分钟；D点时，两人相距50×24=1200米；
设小亮从甲地返回到与小明相遇的时间为第x分钟，
则可得：s=1200+50（x-24）-200（x-24）
化简得：s=-150x+4800，（24≤x≤32）
所以小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式为：s=-150x+4800．
点评 此题考查一次函数的实际运用，注意利用待定系数法求函数解析式．
练习册系列答案
相关题目
5．某校一课外小组准备进行“绿色环保”的宣传活动，需要制作宣传单，校园附近有甲、乙两家印刷社，制作此种宣传单的收费标准如下：
甲印刷社收费y（元）与印制数x（张）的函数关系如下表：
乙印刷社的收费方式为：500张以内（含500张），按每张0.20元收费；超过500张部分，按每张0.10元收费．
（1）根据表中规律，写出甲印刷社收费y（元）与印数x（张）的函数关系式；
（2）兴趣小组决定制作宣传单（已知印数超过500张），若在甲、乙印刷社中选一家，兴趣小组应选择哪家印刷社比较划算？并说明理由．
甲印刷社收费y（元）与印制数x（张）的函数关系如下表：
| 印制x（张） | … | 100 | 200 | 300 | … |
| 收费y（元） | … | 1 | 30 | 45 | … |
（1）根据表中规律，写出甲印刷社收费y（元）与印数x（张）的函数关系式；
（2）兴趣小组决定制作宣传单（已知印数超过500张），若在甲、乙印刷社中选一家，兴趣小组应选择哪家印刷社比较划算？并说明理由．
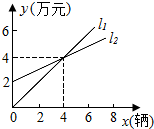如图，l1表示信达商场一天的某型电脑销售额与销售量的关系，l2表示该商场一天的销售成本与电脑销售量的关系，观察图象，解决以下问题：
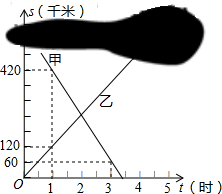甲、乙两列火车分别从A、B两城同时匀速开出，甲车开往B城，乙车开往A城．由于墨迹覆盖，甲车与乙车据B城的距离s（千米）与时间t（小时）的函数关系部分图象如图所示．
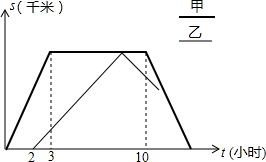甲乙两车从姜堰去往扬州市，甲比乙早出发了2个小时，甲到达扬州市后停留一段时间返回，乙到达扬州市后立即返回．甲车往返的速度都为80千米/时，乙车往返的速度都为40千米/时，下图是两车距姜堰的路程S（千米）与行驶时间t（小时）之间的函数图象．请结合图象回答下列问题：
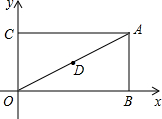如图，在平面直角坐标系中，矩形OBAC的顶点A，B，C的坐标分别为（20，10），（20，0），（0，10）．D为OA的中点，在线段OB上有一动点P，则当PA+PD为最小值时，点P的坐标是（$\frac{40}{3}$，0）．
3．下列事件中，是随机事件的是（ ）
| A． | 对顶角相等 | B． | 内错角相等 | ||
| C． | 三角形内角和等于180° | D． | 等腰梯形是轴对称图形 |
4．
如图所示，正四棱锥的俯视图为（ ）
如图所示，正四棱锥的俯视图为（ ）| A． |  | B． |  | C． |  | D． |  |