题目内容
2.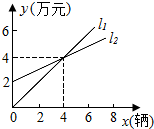 如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:
如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:(1)当x=2时,销售额=2万元,销售成本=3万元,利润(收入-成本)=-1万元;
(2)一天销售4台时,销售额等于销售成本,当销售量大于4时,该商场实现赢利(收入大于成本);
(3)分别求出l1和l2对应的函数表达式;
(4)直接写出利润m与销售量n之间的函数表达式.
分析 (1)设y=kx,根据题意可知当x=4时,y=4,则k=1,即销售收入与销售量之间的函数关系式为y=x;设y=kx+b,把已知坐标代入可得解析式y=$\frac{1}{2}$x+2;代入解析式,得出对应的函数值即可;
(2)由图象可知x>4时,工厂才能获利;
(3)由(1)解答得出函数解析式即可;
(4)可设销售x台时的利润为w万元,由图象可知,当x=2时,w=2-3=-1当x=4时,w=4-4=0,所以可列出方程组,解之即可求出答案.
解答 解:(1)设y=kx,
∵直线过(4,4)两点,
∴4=4k,
∴k=1,
∴y=x;
设y=kx+b,
∵直线过(0,2)、(4,4)两点,
∴2=b,4=4k+2,
∴k=0.5,
∴y=0.5x+2;
把x=2代入y=x=2;
把x=2代入y=0.5x+2=3;
可得当x=2时,销售额=2万元,销售成本=3万元,利润(收入-成本)=2-3=-1万元;
故答案为:2;3;-1;
(2)由图象可得:一天销售4台时,销售额等于销售成本,当销售量大于4台时,该商场实现赢利;
(3)由(1)可得:l1的解析式为y=x;l2的解析式为y=0.5x+2;
(4)设销售x台时的利润为w万元,则:
当x=2时,w=2-3=-1当x=4时,w=4-4=0
所以:$\left\{\begin{array}{l}{2k+b=-1}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=0.5}\\{b=-2}\end{array}\right.$.
所以w=0.5x-2.
点评 本题重点考查了一次函数的图象和性质,也考查了一次函数的应用.此外正确理解题意也是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
7.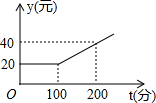 有甲、乙两家通讯公司,甲公司每月通话的收费标准如图①,乙公司每月通话的收费标准如下表:
有甲、乙两家通讯公司,甲公司每月通话的收费标准如图①,乙公司每月通话的收费标准如下表:
(1)根据图、表所提供的信息直接写出甲、乙两家通讯公司的通话费y甲、y乙关于通话时间x(分钟)的函数关系式;
(2)李某准备选择一家通讯公司的服务使用,请问使用那一家公司的费用较低?
 有甲、乙两家通讯公司,甲公司每月通话的收费标准如图①,乙公司每月通话的收费标准如下表:
有甲、乙两家通讯公司,甲公司每月通话的收费标准如图①,乙公司每月通话的收费标准如下表:(1)根据图、表所提供的信息直接写出甲、乙两家通讯公司的通话费y甲、y乙关于通话时间x(分钟)的函数关系式;
(2)李某准备选择一家通讯公司的服务使用,请问使用那一家公司的费用较低?
| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
11.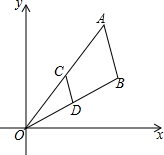 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,4) | D. | ($\frac{7}{2}$,2) |
12.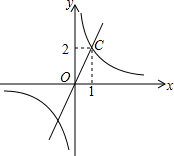 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )| A. | x=1 | B. | x=2 | C. | x1=1,x2=-1 | D. | x1=1,x2=-2 |
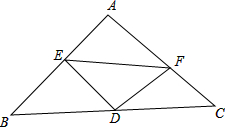 如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.
如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y. 已知:A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,由图象信息得出如下结论:①甲车提速后的速度是60千米/时;②乙车的速度是96千米/时;③点C的坐标为($\frac{19}{6}$,80);④甲车到达B市时乙车已返回A市2小时.你认为正确的结论有( )个.
已知:A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,由图象信息得出如下结论:①甲车提速后的速度是60千米/时;②乙车的速度是96千米/时;③点C的坐标为($\frac{19}{6}$,80);④甲车到达B市时乙车已返回A市2小时.你认为正确的结论有( )个.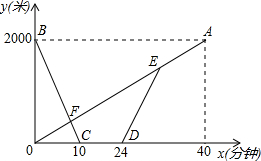 甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.